前回の記事では、リスト(配列)について、解説しました。
リストは、要素の挿入、削除といった操作を行う場合、時間がかかること示しました。
また、リストは要素数が事前に定義が必要でした。
今回は、可変長のデータ構造で、要素の挿入・削除の時間が定数時間で行える、線形リスト及び双方向リストを紹介します。
連結リスト
連結リスト(Linked List)は、以下のようにリストの要素をポインタで繋いだデータ構造です。
線形リストは、線形リスト(Linear List)とも呼ばれます。
連結リストでは、要素数がわかっていない状況でも、連結リストが持つ要素数を可変させることができるので、使用できます。
しかし、ポインタ分の容量が増えるので、リストよりデータ使用量は増えます。Initは先頭のポインタを指します。最後の要素にはNULLを格納し、それ以上先の要素は存在しないことを示します。
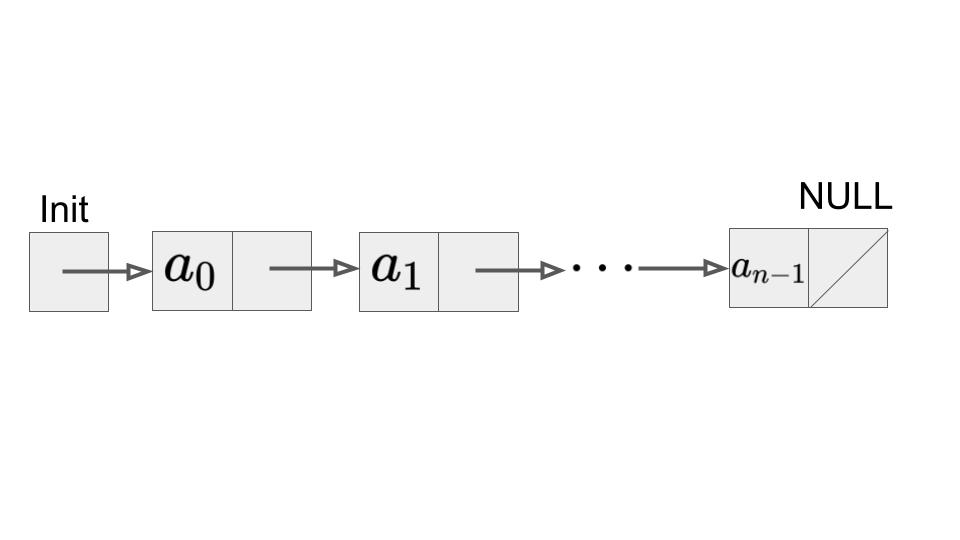
この連結リストに対して、前回記事と同様に、以下の操作を行うことを考えます。
このリストに対して以下の操作を行うことを考えます。
- 位置\(p\)の次の位置に要素\(x\)の挿入:\(Insert(p, x)\)
- 位置\(p\)の次の位置の要素を削除:\(Delete(p)\)
- \(i\)番目の要素の値を取得:\(Locate(i)\)
- 要素\(x\)の検索:\(Find(x)\)
- 最初の位置を取得:\(Top()\)
- 最後の位置を取得:\(Last()\)
- 位置\(p\)の次の位置を取得:\(Next(i)\)
- 位置\(p\)の前の位置を取得:\(Previous(i)\)
順番に一つずつ見ていきましょう。
各種の操作
位置\(p\)の次の位置に要素\(x\)の挿入:\(Insert(p, x)\)
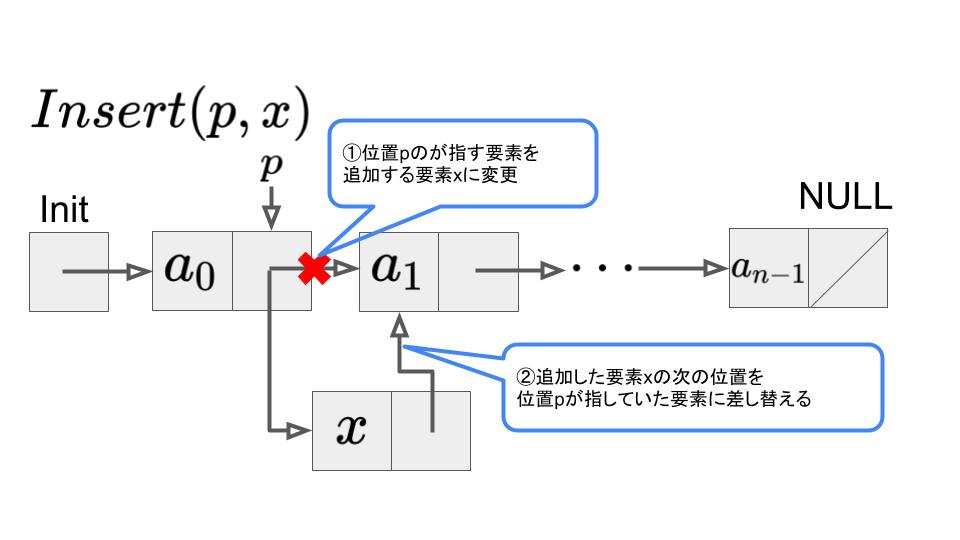
位置\(p\)の次の位置に要素\(x\)の挿入する場合を考えます。この場合、以下の図のように、まず位置pが指す要素を追加する要素に変更します。追加した要素が指す先を、pの次の位置にします。
つまり、ポインタの張り替える操作だけで完結するので、要素数には依存せず定数時間で終了します。
したがって、\(O(1)\)となります。
位置\(p\)の次の位置の要素を削除:\(Delete(p)\)
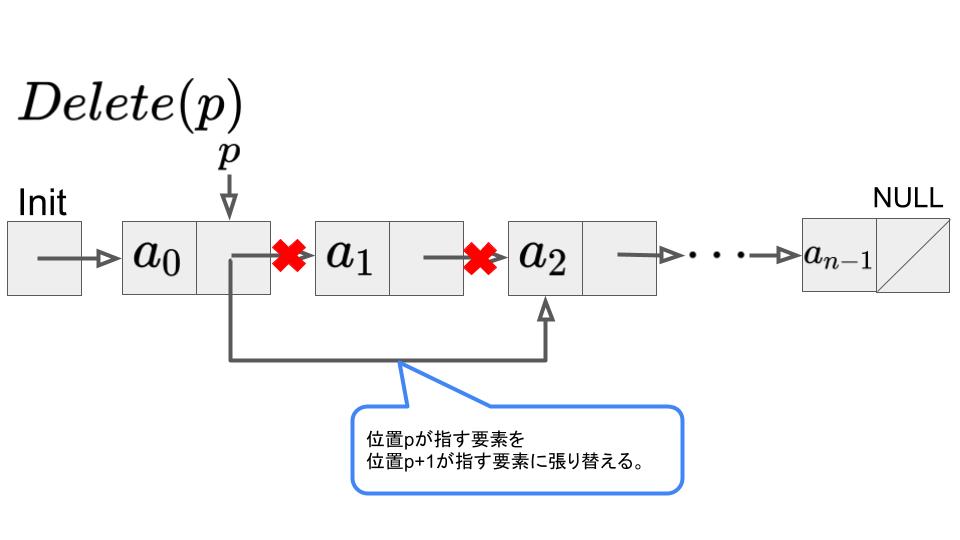
位置\(p\)の次の位置の要素を削除する場合を考えます。
この場合、
追加した要素が指す先を、pの次の位置にします。
\(i\)番目の要素の値を取得:\(Locate(i)\)
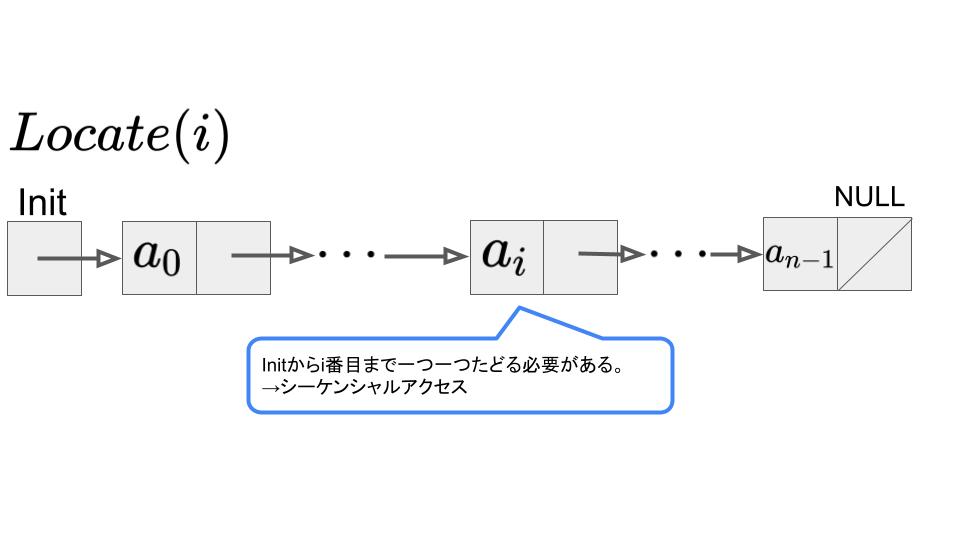
先頭から順にi番目まで、ポインタを辿る必要があるので、最悪の場合\(O(n)\)となります。
つまり、リストと異なりシーケンシャルのアクセス方法となります。
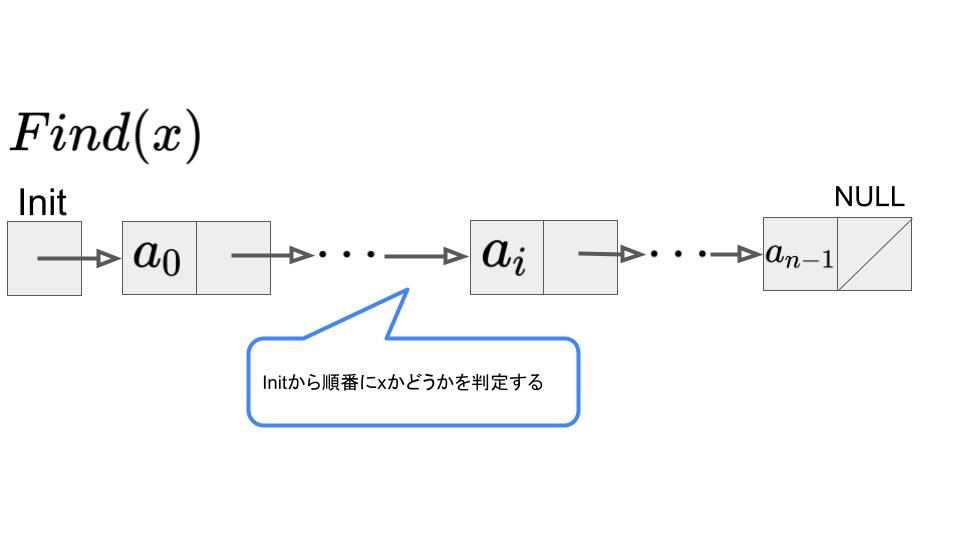
要素\(x\)の検索:\(Find(x)\)
要素xの検索は、Initから順番にxかどうか判定する必要があるので、\(O(n)\)となります。
最初の位置を取得:\(Top()\)
Top()は単純にInitが先頭を指すので、\(O(1)\)で先頭の位置を取得することができます。
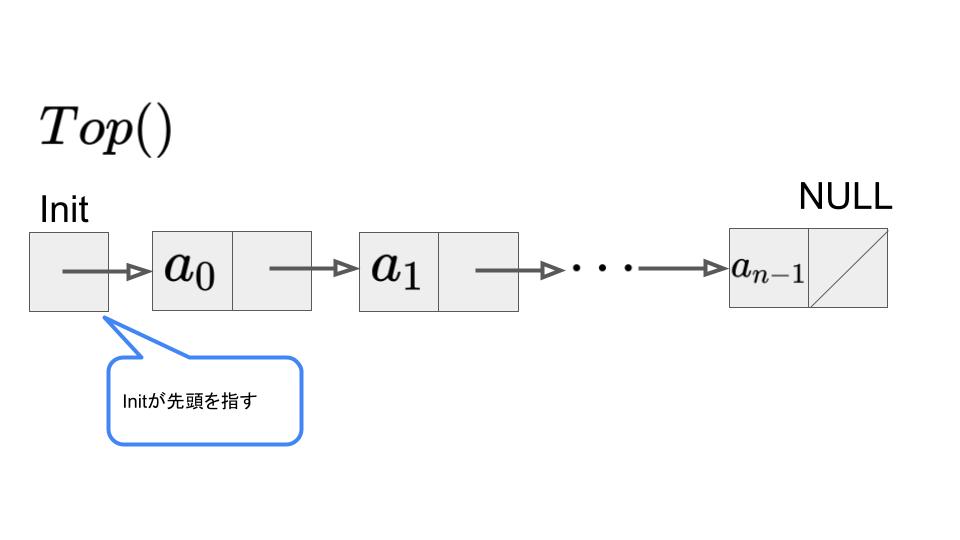
最後の位置を取得:\(Last()\)
最後の位置を取得するには、Initから順番に辿り、次の要素がNULL(辿れなくなる)になるまで、走査する必要があるので\(O(n)\)となります。
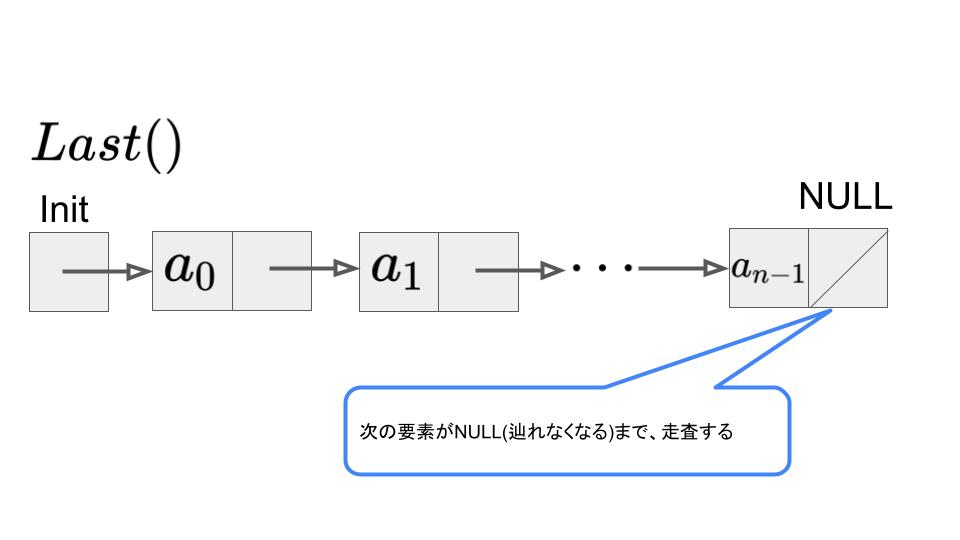
位置\(p\)の次の位置を取得:\(Next(p)\)
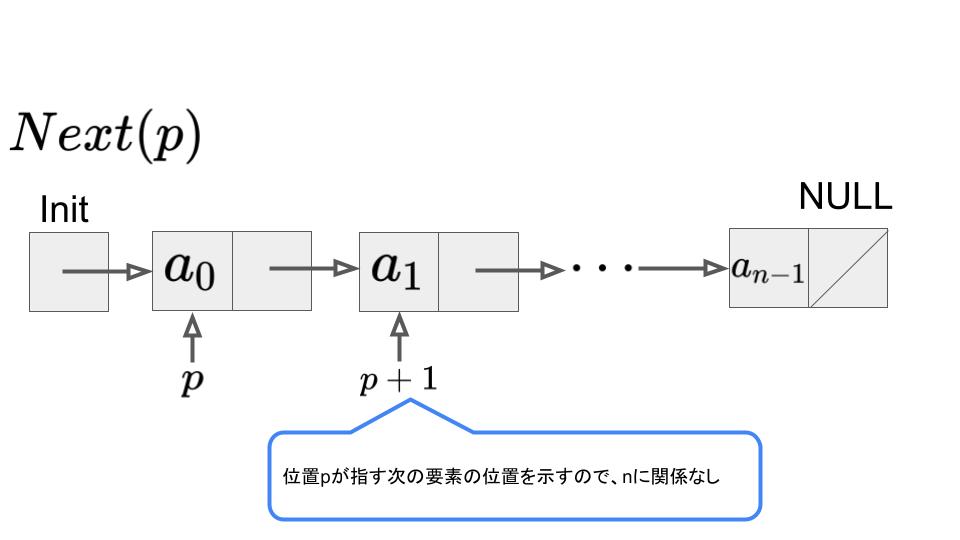
位置pが指す次の要素がp+1になるので、定数時間\(O(1)\)となります。
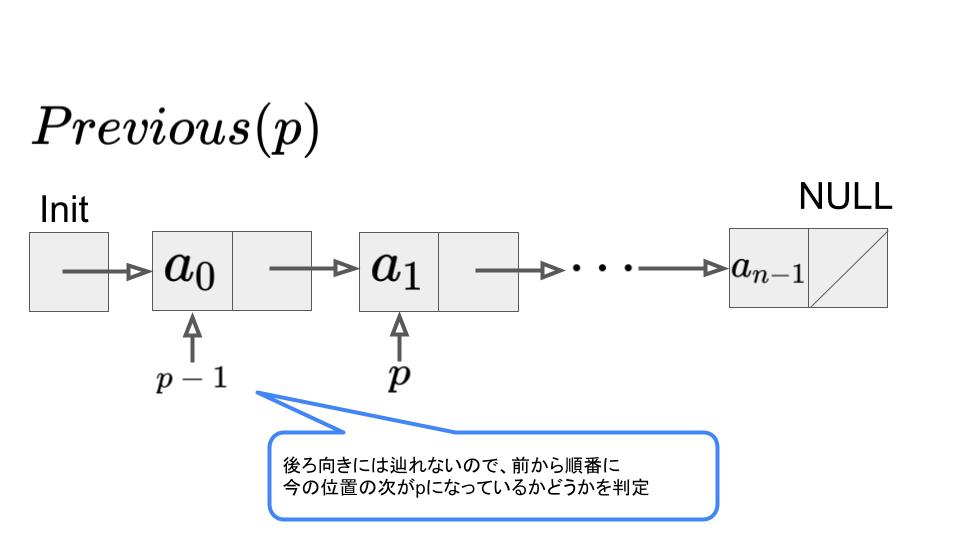
位置\(p\)の前の位置を取得:\(Previous(p)\)
連結リストは、次の要素のポインタしか持たないため、後ろ向きには辿ることができません。
そのため、Initから順番に今の位置がpになっているかどうか判定することで、p-1を取得します。
したがって、\(O(n)\)となります。
双方向リスト(Doubly Linked List)
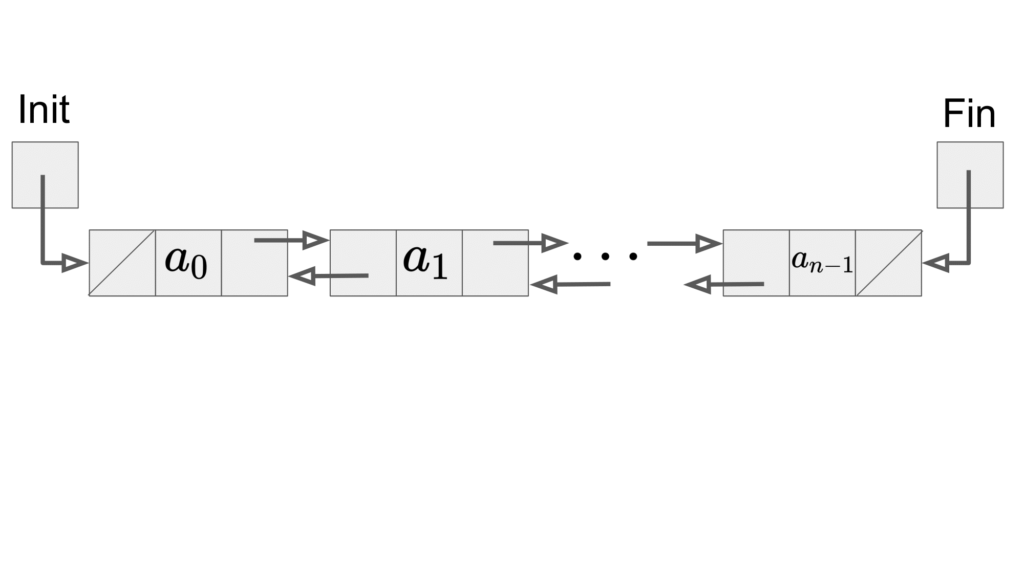
双方向リスト(Linked List)は、連結リストを拡張したデータ構造です。
連結リストは、各要素は次の要素のポインタを持っていましたが、双方向リストは以下の図のように、前の要素のポインタを持つように拡張されています。
連結リストよりもデータ使用量は多くなりますが、連結リストでは時間がかかるPreviousなどが定数時間で行えることが特徴です。
Initは先頭の要素を指すポインタ、Finは最後の要素を指すポインタを表しています。
双方向リストに対しても、以下の操作を行うことを考えます。
- 位置\(p\)の次の位置に要素\(x\)の挿入:\(Insert(p, x)\)
- 位置\(p\)の次の位置の要素を削除:\(Delete(p)\)
- \(i\)番目の要素の値を取得:\(Locate(i)\)
- 要素\(x\)の検索:\(Find(x)\)
- 最初の位置を取得:\(Top()\)
- 最後の位置を取得:\(Last()\)
- 位置\(p\)の次の位置を取得:\(Next(i)\)
- 位置\(p\)の前の位置を取得:\(Previous(i)\)
順番に一つずつ見ていきましょう。
各種の操作
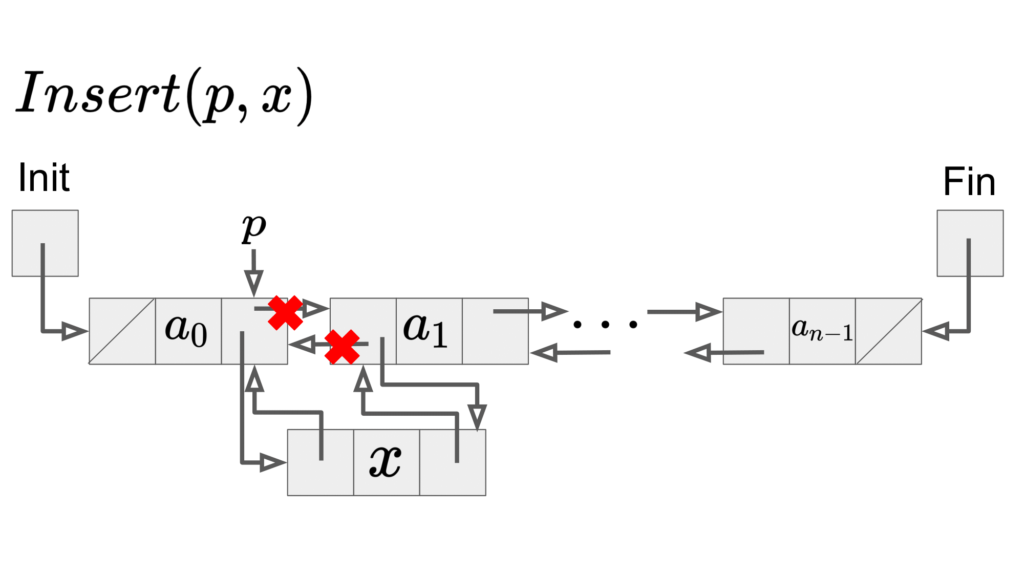
位置\(p\)の次の位置に要素\(x\)の挿入:\(Insert(p, x)\)
双方向リストに、要素を追加する方法は、基本的には連結リストと同じです。異なる点は、ポインタを張り替える部分が2つに増えているという点のみです。
線形リストと同様に、位置pを指定すれば、定数時間で要素追加をできるため、\(O(n)\)となります。
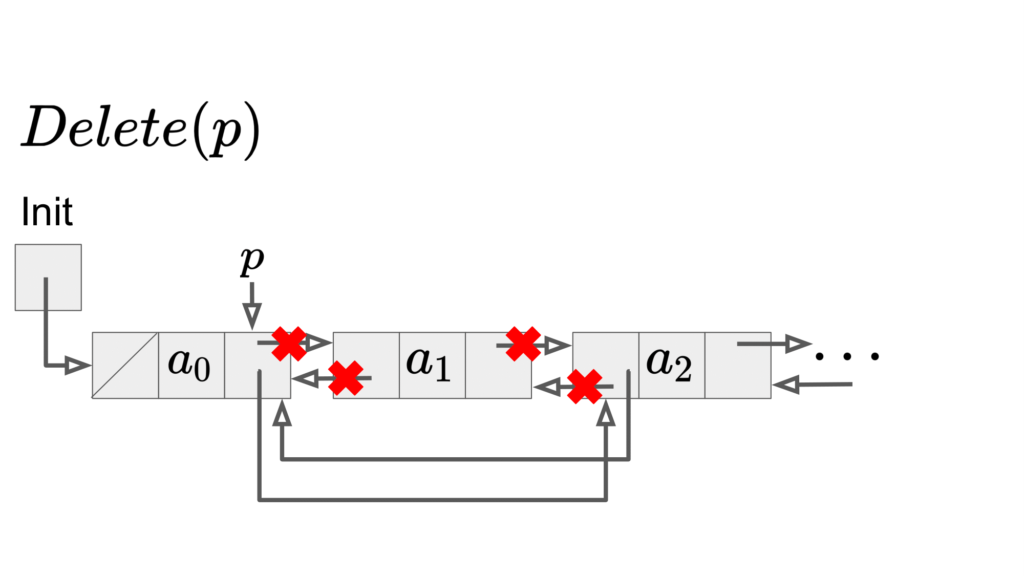
位置\(p\)の次の位置の要素を削除:\(Delete(p)\)
Deleteに関しても、連結リストと同様です。\(O(n)\)となります。
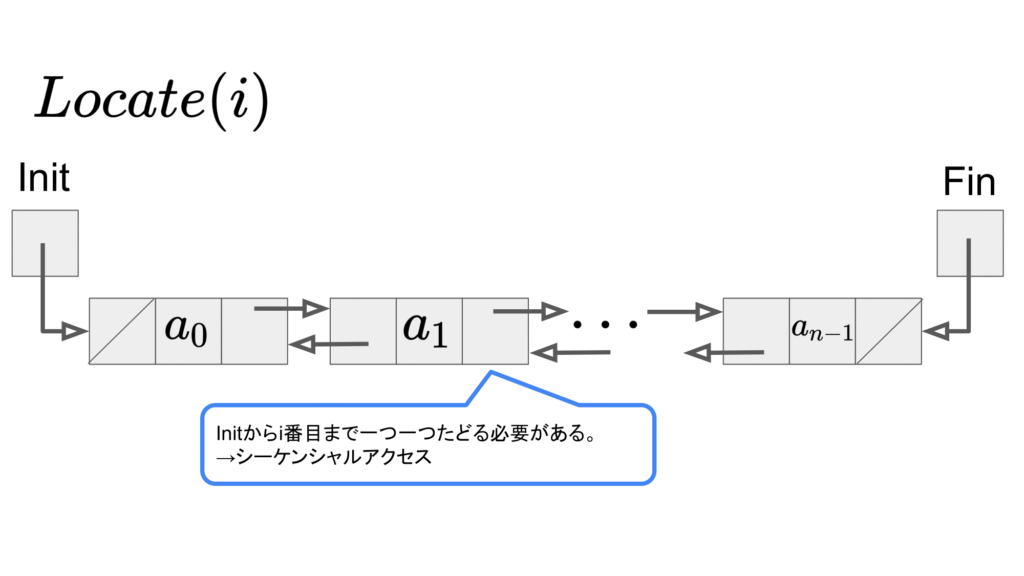
\(i\)番目の要素の値を取得:\(Locate(i)\)
Locateに関しても、Initから順番に辿る必要があるため、\(O(n)\)となります。
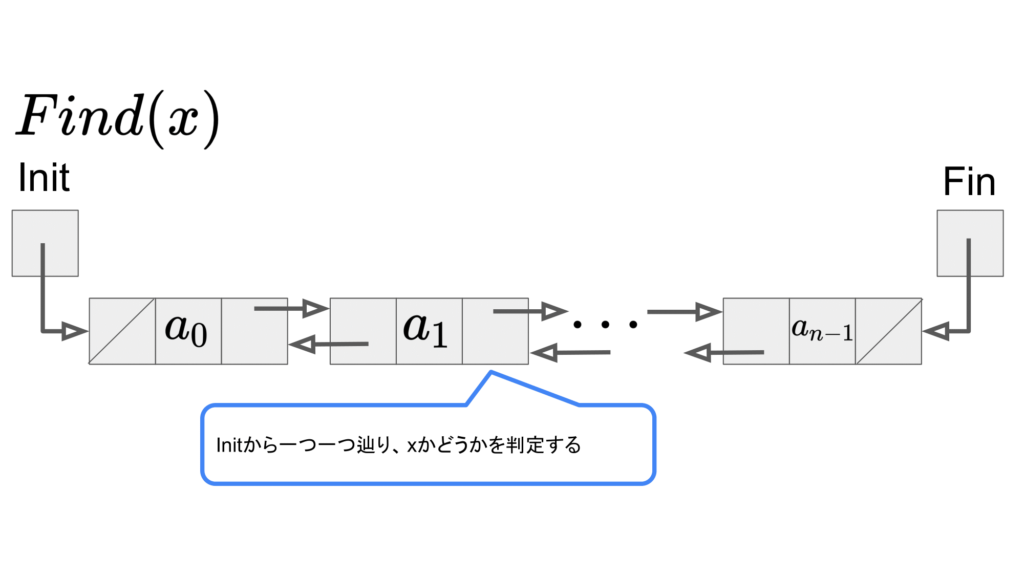
要素\(x\)の検索:\(Find(x)\)
Findに関しても、Initから順番にxかどうか判定する必要があるため、\(O(n)\)となります。
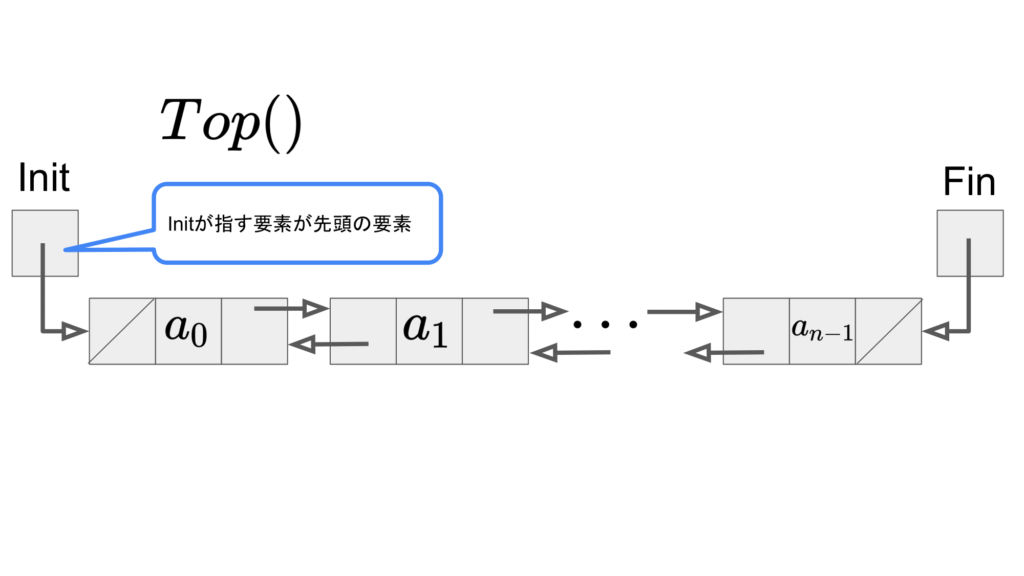
最初の位置を取得:\(Top()\)
Topは、Initが指す要素が先頭の要素になるため、\(O(1)\)となります。
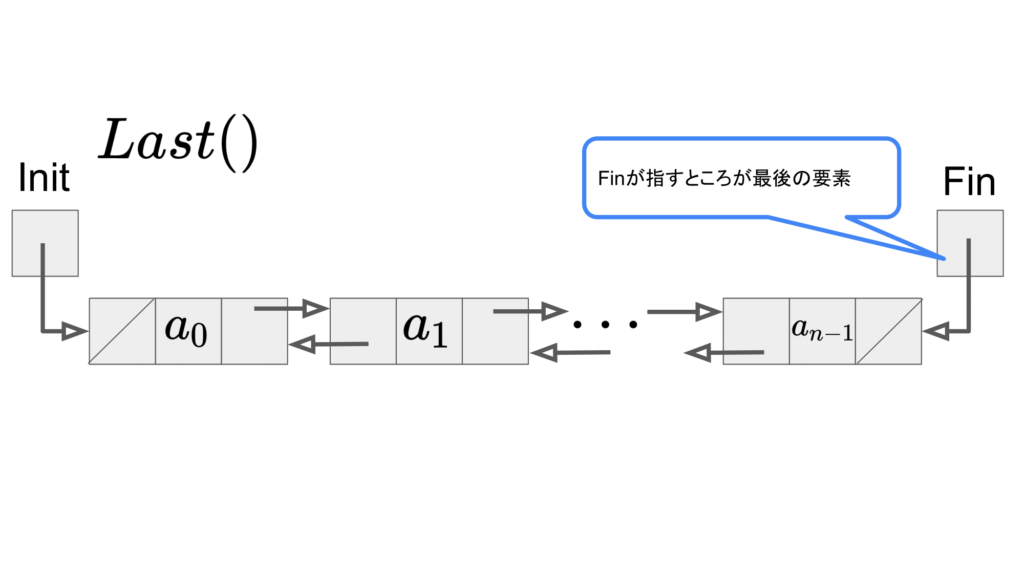
最後の位置を取得:\(Last()\)
今回示した、双方向リストは最後の要素を指すポインタFinを持つため、\(O(1)\)で最後の位置を取得することができます。
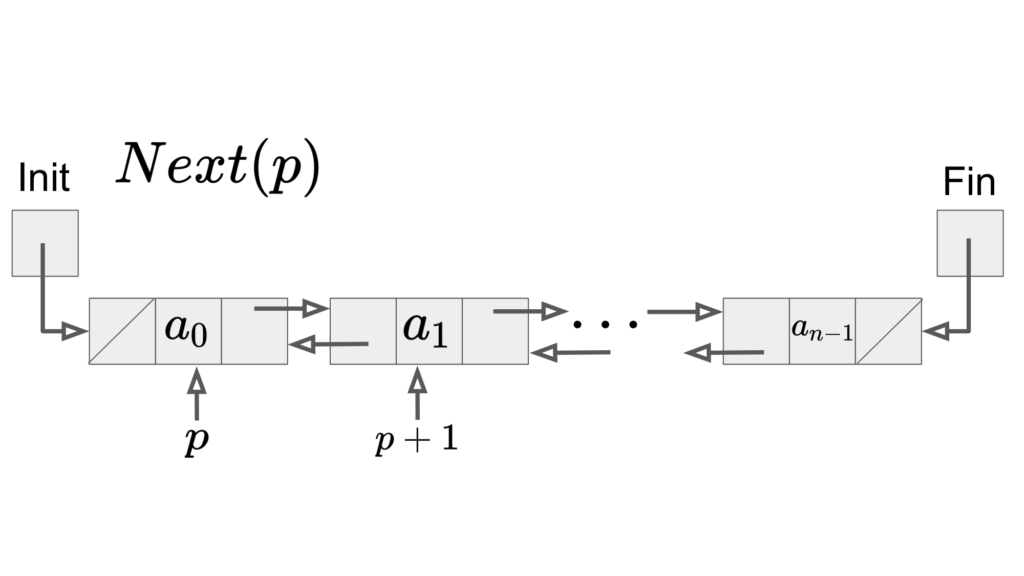
位置\(p\)の次の位置を取得:\(Next(p)\)
双方向リストはpの次の位置、前の位置をそれぞれの要素が持つため、\(O(1)\)で取得できます。
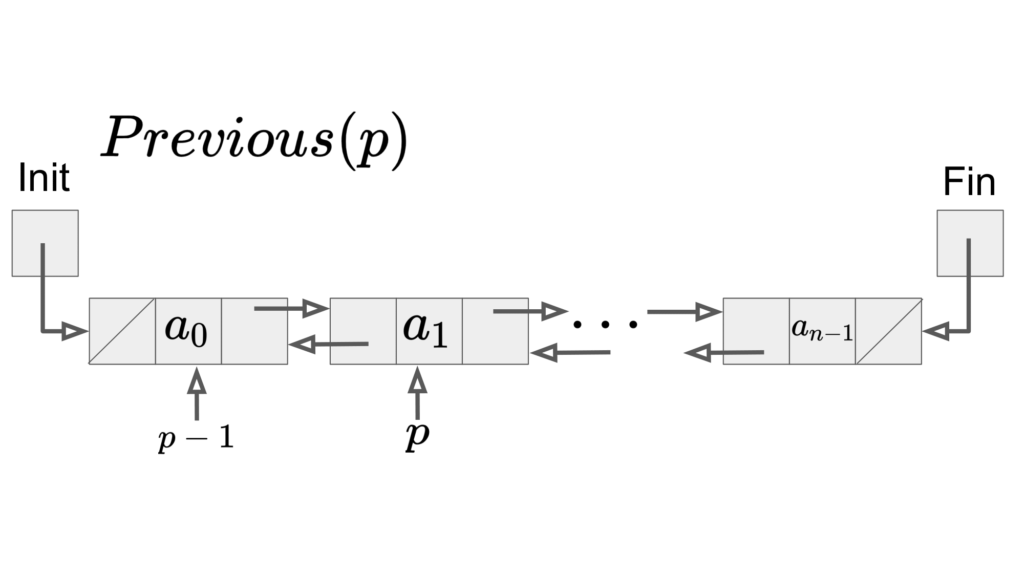
位置\(p\)の前の位置を取得:\(Previous(p)\)
双方向リストはpの次の位置、前の位置をそれぞれの要素が持つため、\(O(1)\)で取得できます。
連結リストは片方向の位置しか持たないので、\(O(n)\)かかっていましたが、双方向リストでは\(O(1)\)で取得可能です。
計算量のまとめ
前回記事の、リストと合わせて、どのような操作に時間がかかるのか以下にまとめておきます。
| リスト | 連結リスト | 双方向リスト | |
| Insert:要素の挿入 | O(n) | O(1) | O(1) |
| Delete:要素の削除 | O(n) | O(1) | O(1) |
| Locate:要素のアクセス | O(1) | O(n) | O(n) |
| Find:要素の検索 | O(n) | O(n) | O(n) |
| Top:先頭の要素 | O(1) | O(1) | O(1) |
| Last:最後の要素 | O(1) | O(n) | O(1) |
| Next:次の要素 | O(1) | O(1) | O(1) |
| Previos:前の要素 | O(1) | O(n) | O(1) |
まとめ
今回、連結リストおよび双方向リストのデータ構造について解説しました。

コメント