今回は、まずデータ構造とは何かについて説明します。その後、基本的なデータ構造の一つであるリスト(配列)について説明します。
データ構造とは
データ構造とは、データの集まりに対して、アルゴリズムの実行を効果的に行うための形式です。それに加えて、「要素の挿入」、「要素の取り出し」などのデータに対する操作も含めてデータ構造と定義されることもあります。
データ構造の重要性
Go言語の開発者である、Rob Pikeもデータ構造の重要性を述べています。
「データは全てを支配する。正しいデータ構造と組織的な物事を上手く選択したとすれば、アルゴリズムは殆どの場合、自明となる。アルゴリズムとは異なりデータ構造はプログラミングの中心である。」
http://users.ece.utexas.edu/~adnan/pike.html
このように、プログラミングにおいてデータ構造の理解は必要不可欠です。
リストについて
要素を0個以上1列に並べたデータ構造をリストと呼びます。多くのプログラミング言語で、配列と呼ばれるデータ構造です。以下の
$$a_0, a_1, \cdots, a_{n-1}$$
のように要素が1列に連続した領域で並んでいるデータ構造です。特に、\(n=0\)のとき空リストと呼びます。
リストの重要な点は、要素数が事前に既知であるということです。
このリストに対して以下の操作を行うことを考えます。
- 位置\(p\)の次の位置に要素\(x\)の挿入:\(Insert(p, x)\)
- 位置\(p\)の次の位置の要素を削除:\(Delete(p)\)
- \(i\)番目の要素の値を取得:\(Locate(i)\)
- 要素\(x\)の検索:\(Find(x)\)
- 最初の位置を取得:\(Top()\)
- 最後の位置を取得:\(Last()\)
- 位置\(p\)の次の位置を取得:\(Next(i)\)
- 位置\(p\)の前の位置を取得:\(Previous(i)\)
順番に一つずつ見ていきましょう。
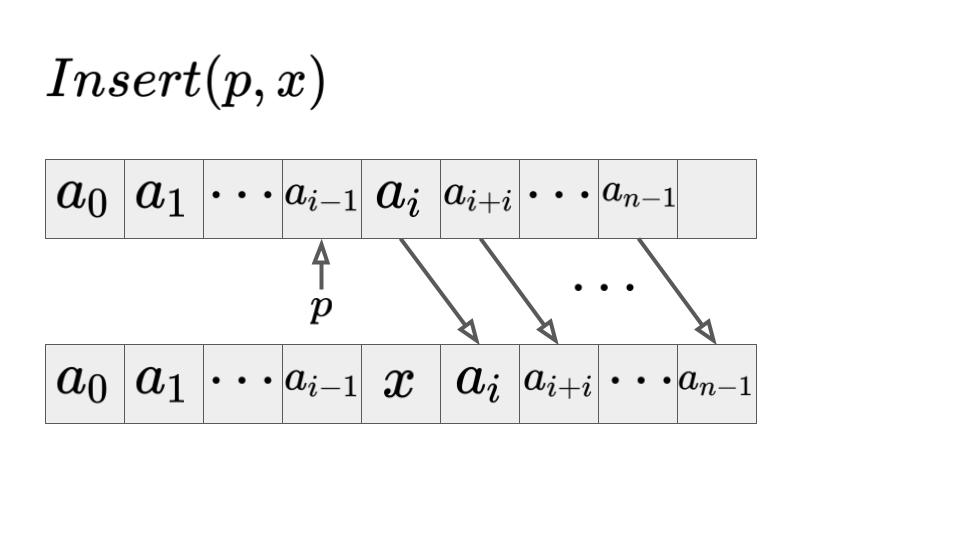
位置\(p\)の次の位置に要素\(x\)の挿入:\(Insert(p, x)\)
\(Insert(p, x)\)は位置pの次の位置に要素xを挿入する場合を考えます。
この場合、最悪の計算量は\(O(n)\)となります。
なぜなら、0番目の要素の位置に要素を追加する場合、その後続のデータ全てを後ろにずらす操作が必要なためです。
位置\(p\)の次の位置の要素を削除:\(Delete(p)\)
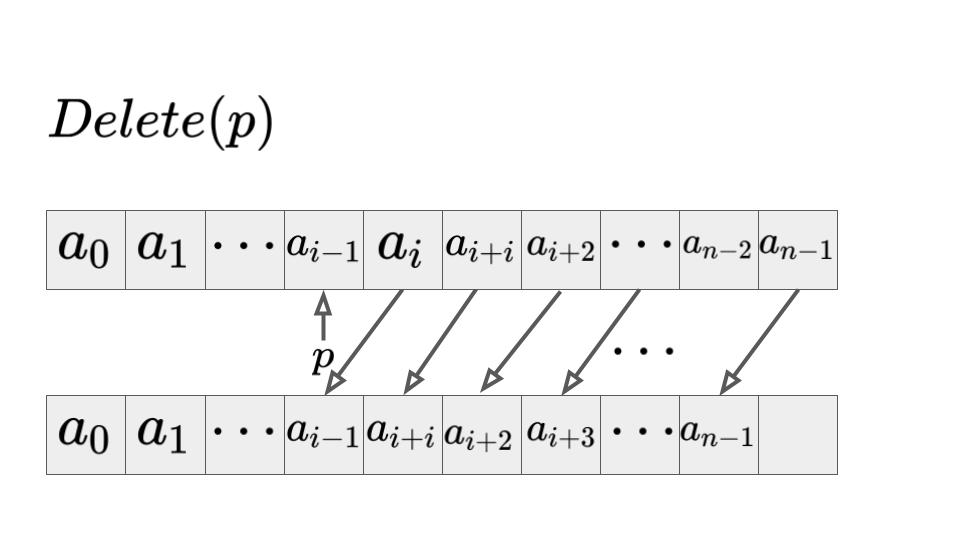
\(Delete(i)\)はi番目の要素を削除する場合を考えます。
この場合、最悪の計算量は\(O(n)\)となります。
なぜなら、0番目の要素を削除する場合、その後続のデータ全てを前にずらす操作が必要なためです。
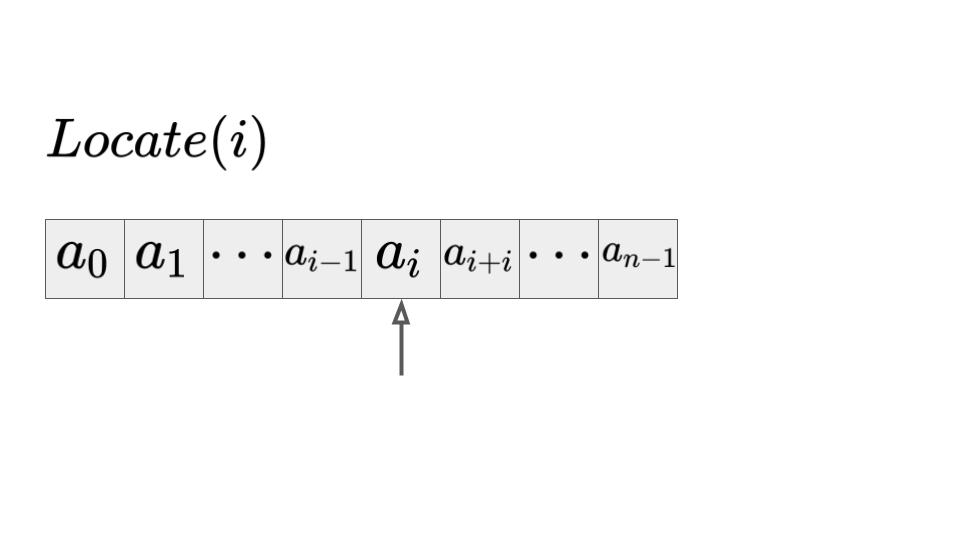
\(i\)番目の要素の値を取得:\(Locate(i)\)
i番目の要素を取得する操作\(Locate(i)\)は、リストは連続領域で格納されているため、位置iがi番目の要素に当たります。つまり、ランダムアクセスが可能なため\(O(1)\)で取得することが可能です。
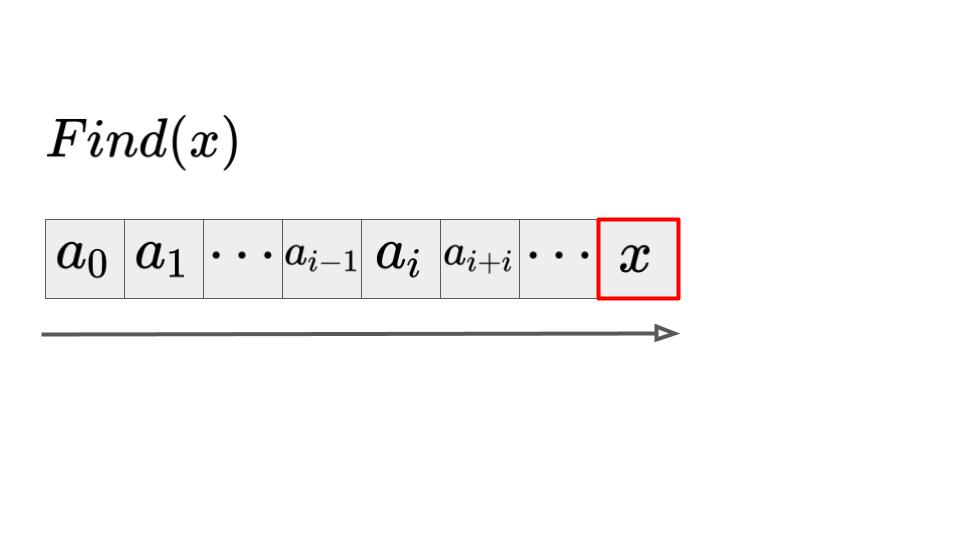
要素\(x\)の検索:\(Find(x)\)
リストに含まれる要素xを検索する\(Find(x)\)は\(O(n)\)の計算量が必要です。
左から右に順番にxかどうか判定し、最後に検索がヒットする場合、一番遅い状態となり\(O(n)\)の計算量となります。
最初の位置を取得:\(Top()\)
最初の位置を取得するのは、単純にリストの0番目が最初の位置になります。したがって、\(O(1)\)となります。

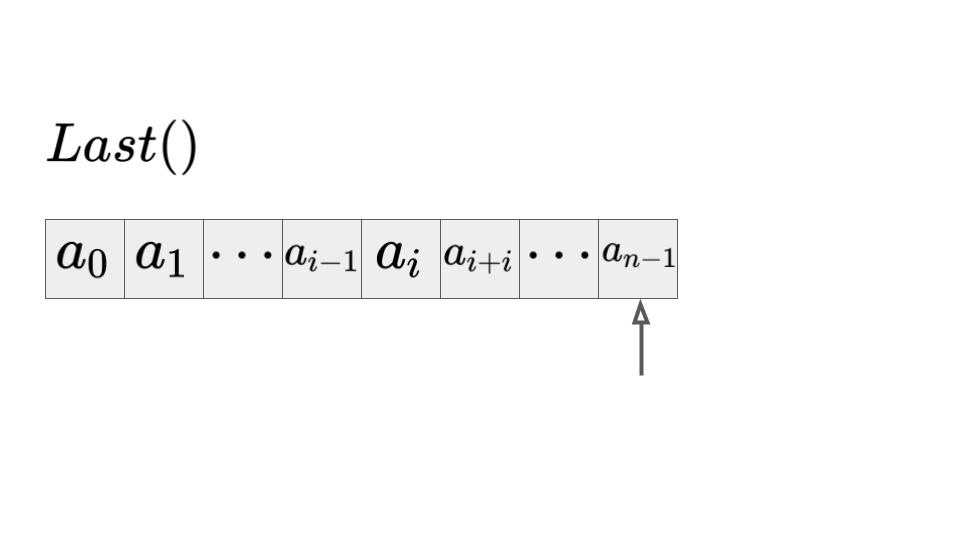
最後の位置を取得:\(Last()\)
最後の位置はn-1番目になります。したがって、\(O(1)\)となります。
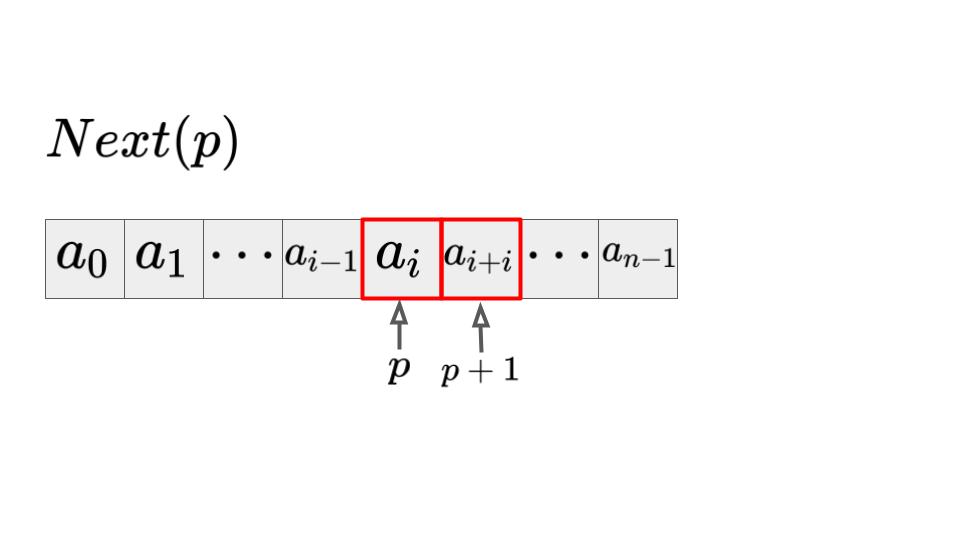
位置\(p\)の次の位置を取得:\(Next(p)\)
位置pの次の位置を取得するには、単純に指定したインデックスの次の要素にアクセスするだけなので、\(O(1)\)となります。
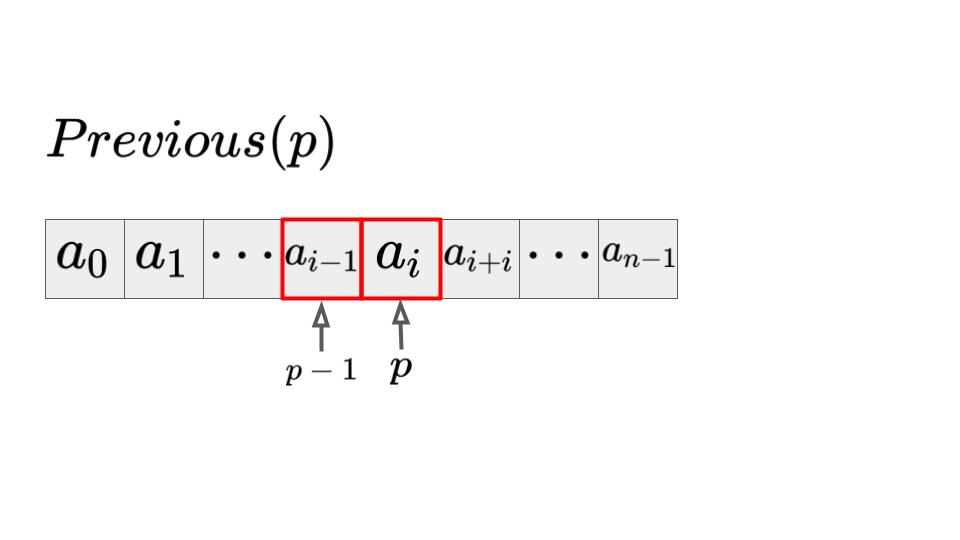
位置\(p\)の要素の前の値を取得:\(Previous(p)\)
位置pの前の位置を取得するには、単純に指定したインデックスの前の要素にアクセスするだけなので、\(O(1)\)となります。
まとめ
以上の各操作の計算量を表にまとめます。
表から分かるように、リストというデータ構造は、要素の挿入、削除、検索といった操作に時間がかかることがわかります。
| Insert:要素の挿入 | O(n) |
| Delete:要素の削除 | O(n) |
| Locate:要素のアクセス | O(1) |
| Find:要素の検索 | O(n) |
| Top:先頭の要素 | O(1) |
| Last:最後の要素 | O(1) |
| Next:次の要素 | O(1) |
| Previos:前の要素 | O(1) |

コメント