以前、1ビット同士の加算を実現する全加算器を解説しました。この1ビットの全加算器を桁数分だけ並べることで、複数ビットの加算を行うことができます。この方式で複数ビットの加算器としたものを桁上げ伝播加算器(CRA: Carry Ripple Adder)といいます。

桁上げ伝播加算器(Carry Ripple Adder)
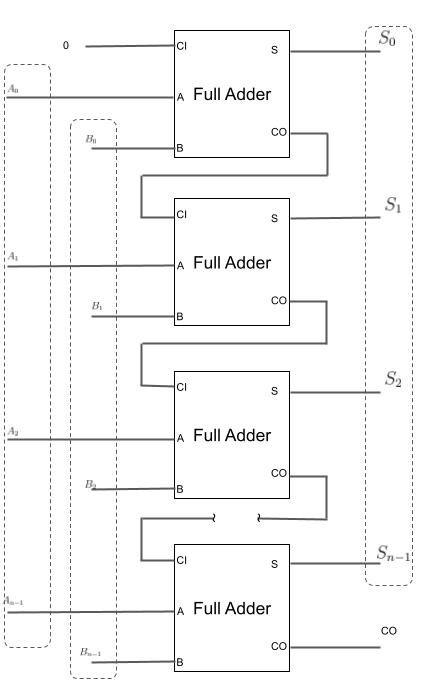
キャリーリップルアダーCRAは下図のように表されます。nビットのCRAは第iビットの上位ビット(i+1)ビットの桁上げ入力はその第iビットの桁上げ出力なので、
$$CI_{i+1} = CO_{i} (i = 0, \cdots, n-2)$$
となります。ただし、最下位ビット(LSB)の桁上げ入力CIは加算器全体への桁上げ入力CIであり、最上位ビット(MSB)の桁上げCOは加算器全体の桁上げ出力である。LSBのCIに0を入力するとnビットの加算回路となる。
この方式では、最下位ビットの桁上がりが2ビット目の加算に使われる。さらに2ビット目の加算結果が3ビット目の桁あがりの入力に使われる。これが最上位ビットまで繰り返してキャリーを伝播させていくのがわかります。このようなキャリーの伝わり方が、キャリーリップルと呼ばれています。
この方式は、多数桁の筆算と同じように、最下位桁から計算していき、最上位桁まで加算していくというものと同様で、2進数版と考えればわかりやすいです。
CRAの特徴
CRAには全加算器をbit数分接続するだけで、複数bitの加算が実現できるため、回路が簡単であるという長所があります。一方で、桁数に比例して伝播遅延時間が大きくなるという欠点があります。4ビットや8ビットなどのビット数であればそこまで大きな問題にはなりませんが、現代のCPUでは32ビットや64ビットの計算を基本としているので、この伝播時間が無視できない大きさになってきます。また、加算は使用頻度が非常に高い演算なので、加算の速度は性能への影響が大きいです。
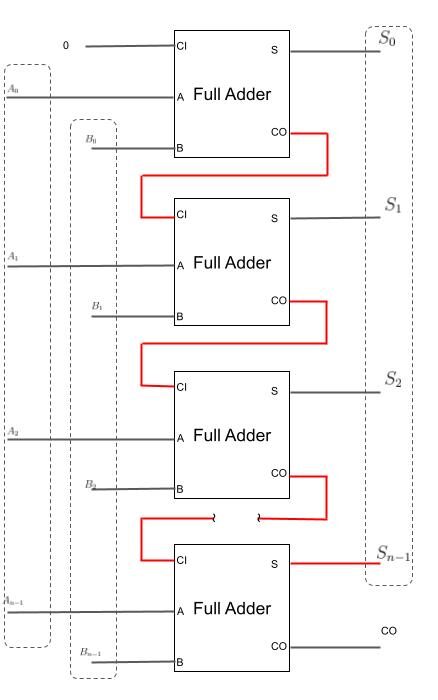
実際のディジタル回路は入力してから出力するまで遅延があります。また、配線の遅延も発生するので、下図の赤線のように、下位ビットの出力が確定するまで上位ビットの出力が確定しないような構成になってしまうと扱うビット数が増えるほど遅延が増えてしまいます。
まとめ
本記事では、複数ビットの加算を行うCRAを解説しました。CRAは回路が簡単である一方で、扱うビット数に比例して遅延時間が増加するという欠点があります。



コメント