ピンホールカメラモデルと透視投影モデル

本記事では、画像処理で基本となるカメラ画像のモデル化について解説します。

ピンホールカメラモデル

ピンホールカメラモデルは、光がピンホールと呼ばれる小さな穴を通って作る像をモデル化したものである。ピンホールカメラモデルでは、光学中心を通る光線だけで投影面への結像をモデル化しています。投影面は実際に画像が投影されている面のことです。モデルのパラメータは光学中心から投影面までの焦点距離\(f\)です。

ピンホールカメラモデルは以下の図のように表すことができます。この図からも投影面に結像している像は上下・左右反転していることがわかります。

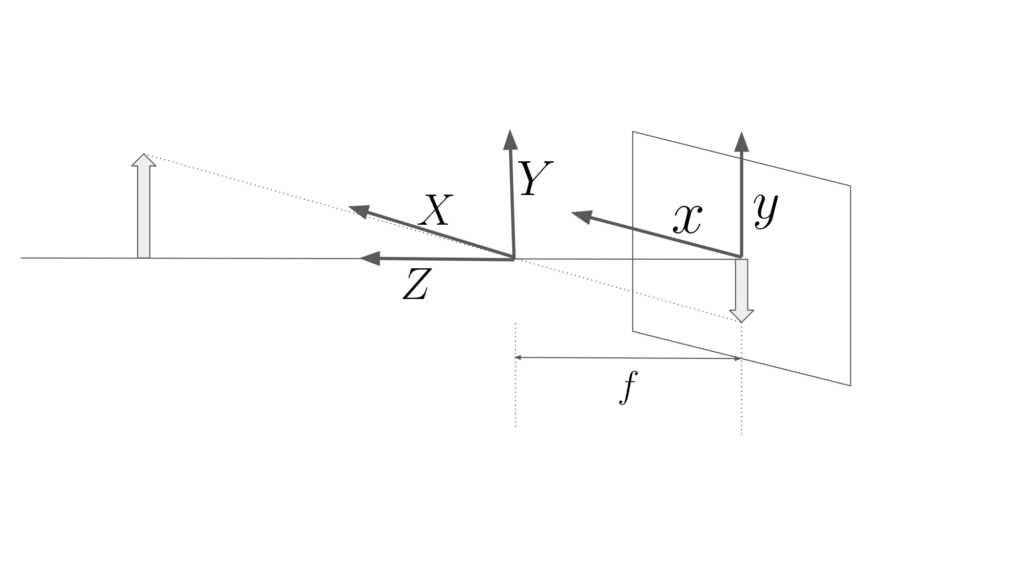
ここで、求めたいのはカメラで観測している座標軸である\((X, Y, Z)\)から投影面での\((x, y)\)です。これらを求めるために三角形の相似の関係を利用します。上の図は、以下の図のように三角形の相似の関係を利用して次の関係が導けます。

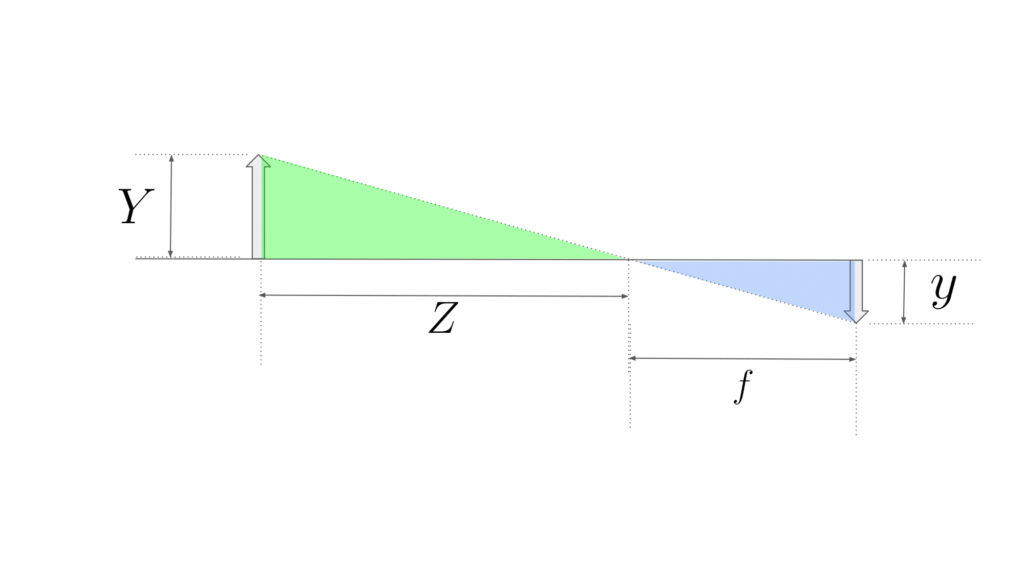
$$Y:Z = y: f$$

従って、

$$y = f\frac{Y}{Z}$$

という式が得られます。同様に\(x\)も左右反転して像が結像されていることを考慮し求めると、

$$X:Z = x: f $$

より、

$$x = f\frac{X}{Z}$$

という関係式が得られます。

ここで、上の図を見ると、像は\(y\)軸が反転して結像されていることがわかります。図上には表れていないが、ピンホールカメラモデルでは\(x\)軸も反転して結像されています。このこと反転していることを考えると、上の式は次のように表すことができます。

$$y = -f\frac{Y}{Z}, x = -f\frac{X}{Z}$$

これは\(x\)軸と\(X\)軸、\(y\)軸と\(Y\)軸が同じ向きに設定されているため、負の値になっています。この式はWebページや教科書によっては、座標系が以下のように、あらかじめ反転を考慮した取り方になっていることがあります。この場合は、負の値にはならず、

$$y = f\frac{Y}{Z}, x = f\frac{X}{Z}$$

という関係式になります。

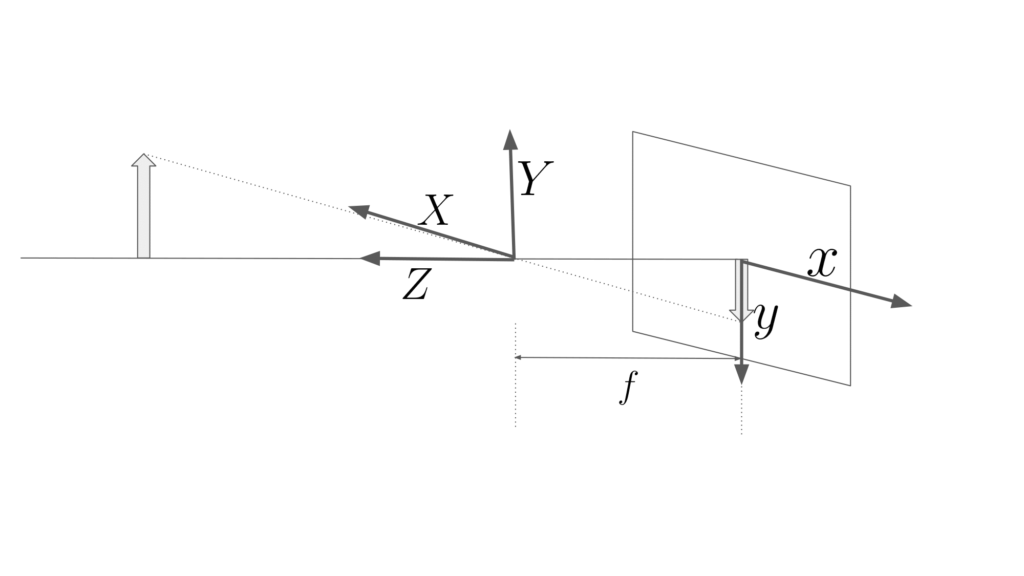
座標系の向きに注意して読み進めるようにしましょう。

透視投影モデル

前節では、ピンホールカメラモデルについて解説しました。ピンホールカメラモデルでは、画像の座標軸とカメラの座標軸が反転していることを説明しました。実際の像と投影面に写る像は上下左右反転することは、直感的にわかりずらいです。そこで、実際の像と投影面に写る像を同じ向きにしようということが考えられます。実際には、ピンホールカメラモデルで示した位置で像は結像されるのですが、計算機上で扱いやすいように投影面が同じ向きになる位置で仮想的に投影されていることを考えます。このようなモデルを透視投影モデルと呼びます。

以下の図のように、光学中心より前の位置に投影面が存在していることがわかります。また、図より投影面自体が上下左右反転し、軸の取り方も変わっていることに注目してください。このよなモデルを考えることで、ピンホールカメラモデルでは\(x\)軸と\(X\)軸、\(y\)軸と\(Y\)軸が左右対称なため符の値となっていたが、それらが解消されています。

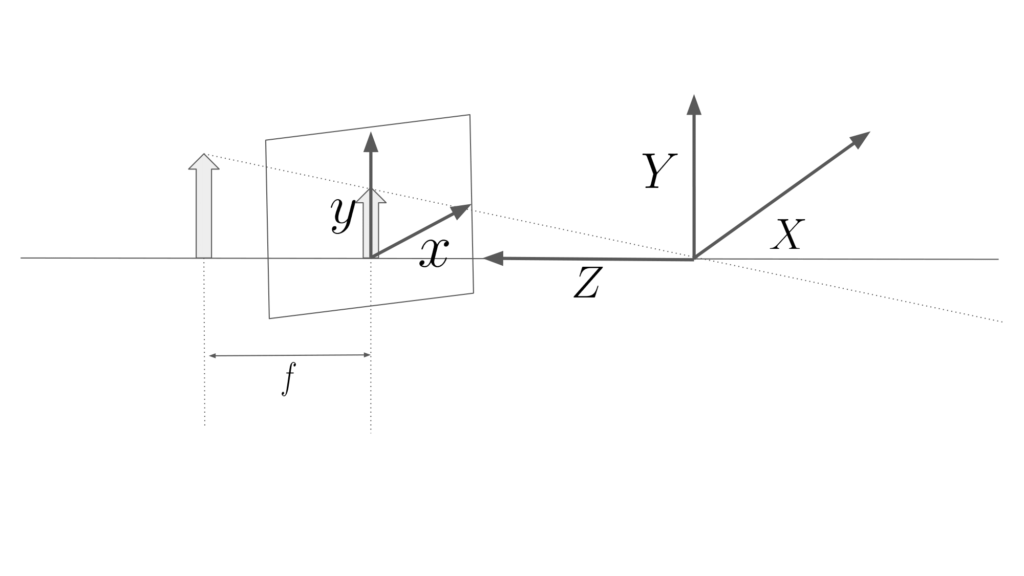
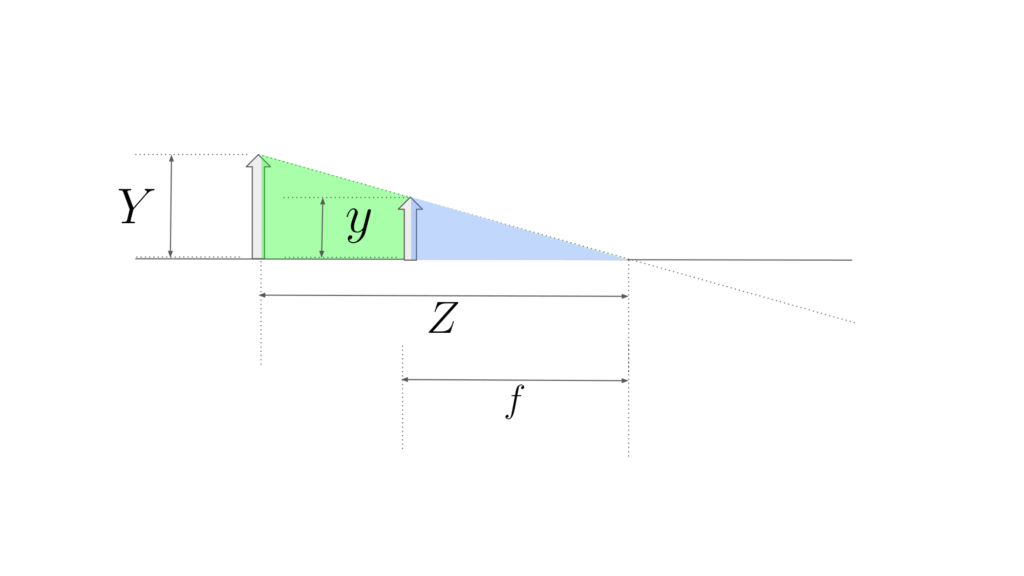
上の図でも、同じように三角形の相似を利用して対応関係を求めることができます。以下の図より、対応関係は次式で求めることができます。

$$y = f\frac{Y}{Z}, x = f\frac{X}{Z}$$

まとめ

本記事では、ピンホールカメラモデルと透視投影モデルについて説明しました。3次元の座標空間\((X, Y, Z)\)から投影面での\((x, y)\)座標空間へ対応づける関係式を導出しました。