t-SNEは、データ可視化のために、低次元空間への埋め込みに最適な非線形の次元削減手法の一つです。教師なし学習のひとつで、SNEという次元削減アルゴリズムを改良した手法です。
PCAと異なり、PCAでは表現できな非線形なデータ、かつ高次元なデータに対しても、データ関係を学習することができ、次元削減が可能になります。
目次
t-SNEの使い方
【TSNE()の引数】
- n_components:削減次元数(デフォルトは2)
- perplexity:最近傍の数(デフォルトは30)
- early_exaggeration:密集度合の設定(デフォルトは12.0)
- learning_rate:t-SNEの学習率(デフォルトは200.0)
- n_iter:最適化の最大反復回数(デフォルトは1000)
- random_state: 乱数
- n_jobs: 並列処理する場合の多重度(デフォルトは1)
【クラスのメソッド】
- fit(X):計算の実行
- fit_transform(X): 変換された出力を表示する
次元削減をして可視化
ライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.manifold import TSNEデータセットの準備
iris_df = load_iris(as_frame=True).frame
X = iris_df.drop("target", axis=1).values
y = iris_df.target.values3次元の可視化
tsne = TSNE(n_components=3, random_state=42, init="pca", learning_rate="auto")
X_decompose = tsne.fit_transform(X)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(X_decompose[y==0,0], X_decompose[y==0,1], X_decompose[y==0,2], marker="o", s=40)
ax.scatter(X_decompose[y==1,0], X_decompose[y==1,1], X_decompose[y==1,2], marker="^", s=40)
ax.scatter(X_decompose[y==2,0], X_decompose[y==2,1], X_decompose[y==2,2], marker="+", s=40)
plt.show()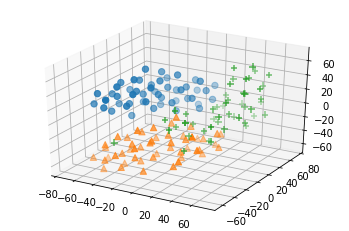
2次元の可視化
tsne = TSNE(n_components=2, random_state=42, init="pca", learning_rate="auto")
X_decompose = tsne.fit_transform(X)
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(X_decompose[y==0,0], X_decompose[y==0,1], marker="o", s=40)
ax.scatter(X_decompose[y==1,0], X_decompose[y==1,1], marker="^", s=40)
ax.scatter(X_decompose[y==2,0], X_decompose[y==2,1], marker="+", s=40)
plt.show()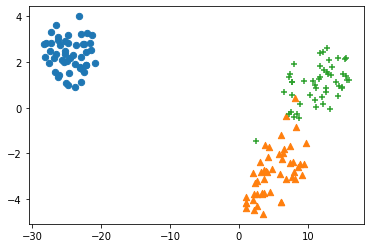
まとめ
本記事では、t-SNEを使用して特徴量の次元削減を行いました。次元削減により、高次元の特徴量が可視化することができ、それらの方法について紹介しました。



コメント