主成分分析(PCA:Principal Component Analysis)は教師なし学習の一つのアルゴリズムです。主成分とは、相関のない少数で全体のばらつきを最もよく表す変数のことをいいます。PCAを行うことにより、特徴量の次元を削減することができ、データの特徴が判断しやすくなります。
PCAのフロー
- データの重心を求める
- 重心からデータの分散が最大となる方向を見つける
- 2で求めた方向を新たな基底とする。
- 3で作成した基底と直交する方向に対して分散最大となる方向を探す
- 元データの次元数だけ繰り返す
目次
PCAの使い方
PCAのインスタンスを作成する際の基本的な引数が以下となります。
- n_components:圧縮後の次元数
- copy:Falseの場合、変換するデータを上書きする(デフォルトはTrue)
- whiten: Trueの場合、白色化とよばれる、変数間の相関をなくす処理を行う(デフォルトはFalse)
- svd_solver: 特異値分解のソルバ(‘auto’, ‘full’, ‘arpack’, ‘randomized’)
- random_state: 乱数
また、作成したインスタンへの基本的なメソッドは以下となります。
- fit(X):学習の実行
- fit_transform(X):PCA変換
- transform(X): fitやfit_transformで定義したPCA変換
- sinverse_transform(X): PCAの逆変換
次元削減をして可視化
ライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCAデータセットの準備
iris_df = load_iris(as_frame=True).frame
X = iris_df.drop("target", axis=1).values
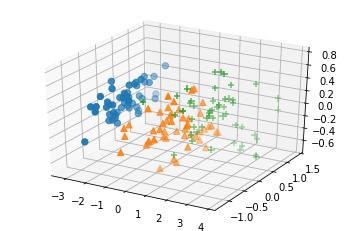
y = iris_df.target.values3次元の可視化
pca = PCA(n_components=3)
X_decompose = pca.fit_transform(X)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(X_decompose[y==0,0], X_decompose[y==0,1], X_decompose[y==0,2], marker="o", s=40)
ax.scatter(X_decompose[y==1,0], X_decompose[y==1,1], X_decompose[y==1,2], marker="^", s=40)
ax.scatter(X_decompose[y==2,0], X_decompose[y==2,1], X_decompose[y==2,2], marker="+", s=40)
plt.show()
2次元の可視化
pca = PCA(n_components=2)
X_decompose = pca.fit_transform(X)
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(X_decompose[y==0,0], X_decompose[y==0,1], marker="o", s=40)
ax.scatter(X_decompose[y==1,0], X_decompose[y==1,1], marker="^", s=40)
ax.scatter(X_decompose[y==2,0], X_decompose[y==2,1], marker="+", s=40)
plt.show()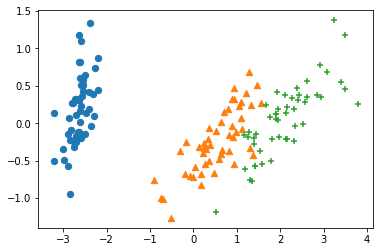
まとめ
本記事では、PCAを使用して特徴量の次元削減を行いました。次元削減により、高次元の特徴量が可視化することができ、それらの方法について紹介しました。



コメント