論理回路で加算を実現するのが加算回路です。加算回路は組み合わせ回路なので、組み合わせ回路の設計で導出できます。
半加算器(Half Adder)
まず、簡単のため1桁同士の加算を考えます。加算はS = A+Bという2の入力と1つの出力から構成されます。ここで、2進数で1 + 1 = 10の桁上げに対応するため、1つの出力を追加します。したがって、2入力2出力の回路になります。これを真理値表で表すと以下のようになります。上位桁の桁上げをCとしています。
| A | B | S | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
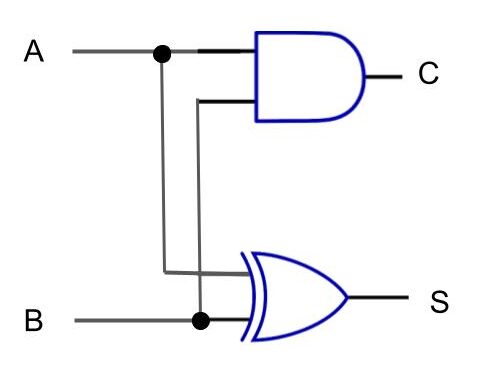
真理値表からCは排他的論理和と同等、Sは論理積と同等ということがわかります。ブール代数で表すと次式になります。
$$S = A\oplus B$$
$$C = A \cdot B$$
回路図で表すと以下のようになります。
このような1桁同士の加算を行う回路を半加算器と呼びます。
なぜ、半加算器と呼ばれるのかは桁上がりを考慮していないことによります。2桁以上の加算を実現するためには、下位の桁からの桁上がりを考慮する必要があります。この桁上がりを考慮し、1桁の加算を行う回路を全加算器と呼びます。
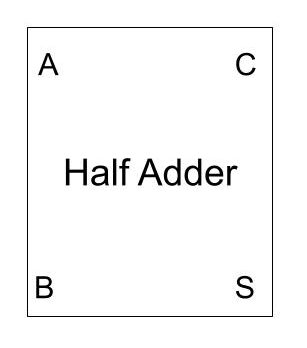
このような半加算器は簡略化して、以下のように表すことがあります。
全加算器(Full Adder)
全加算器は、半加算器に対して、桁上がりを考慮したものでした。桁上げを考慮すると、S = A+B+CI(CI:下位の桁からの桁上げ)、CO(上位桁への桁上げ)となります。したがって、桁上がりの入力が一つ増えるので、3入力2出力になります。
これを真理値表で表すと以下のようになります。
| A | B | CI | S | CO |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
全加算器の論理式
全加算器の真理値表を加法標準形で表すと以下のようになります。
$$S = \bar{A}\cdot\bar{B}\cdot CI + \bar{A}\cdot B\cdot\overline{CI} + A\cdot\bar{B}\cdot\overline{CI} + A\cdot B\cdot CI$$
$$CO = \bar{A}\cdot B\cdot CI + A\cdot\bar{B}\cdot CI + A\cdot B\cdot \overline{CI} + A\cdot B\cdot CI$$
上の式を変形します。まずは、加算の出力結果であるSはCIで括ると
$$S = ( \bar{A}\cdot\bar{B} + A\cdot B ) CI + ( \bar{A}\cdot B + A\cdot \bar{B} ) \overline{CI} $$
となります。ここで、
$$A\oplus B = \bar{A}\cdot B + A\cdot \bar{B} $$
$$\overline{A\oplus B} = \bar{A}\cdot B + A\cdot \bar{B} $$
なので、
$$ = (\overline{A\oplus B}) CI + (A\oplus B)\overline{CI}$$
となります。ここで、\( X= A\oplus B\)と置くと、
$$ = \bar{X} CI + X \overline{CI} $$
となるので、これもまた排他的論理和と同じなので
$$S = X\oplus CI = (A\oplus B)\oplus CI$$
となります。
次に、桁上げの式を変形をします。
$$CO = \bar{A}\cdot B\cdot CI + A\cdot\bar{B}\cdot CI + \bar{A}\cdot\bar{B}\cdot CI + A\cdot B\cdot CI$$
CIで括ると
$$(\bar{A}\cdot B + A\cdot\bar{B})\cdot CI + A\cdot B\cdot CI + A\cdot B \cdot \overline{CI}$$
となり、ここで、\(A\oplus B = \bar{A}\cdot B + A\cdot \bar{B}\)なので、
$$ = (A\oplus B)\cdot CI + A\cdot B\cdot CI + A\cdot B \cdot \overline{CI}$$
$$ = (A\oplus B)\cdot CI + A\cdot B \cdot (CI + \overline{CI})$$
ここで、\(X + \bar{X} = 1\)(補元律)を利用すると、次式のようになります。
$$CO = (A\oplus B)\cdot CI + A\cdot B$$
まとめると、
$$S = (A\oplus B)\oplus CI$$
$$CO = (A\oplus B)\cdot CI + A\cdot B$$
となります。
全加算器の設計
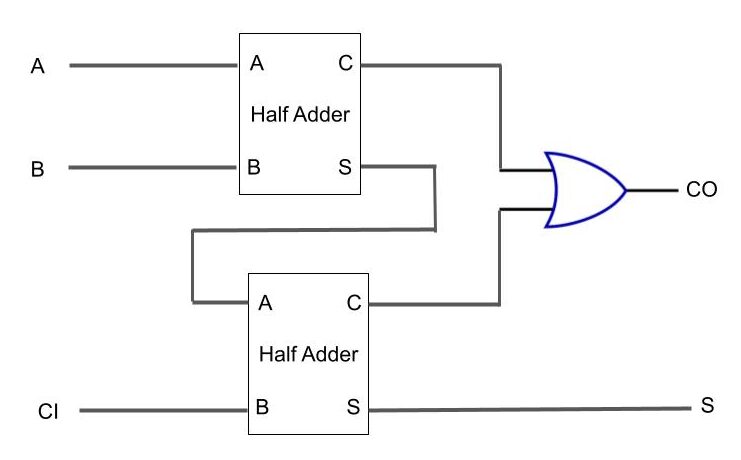
全加算器の論理式から、全加算器の出力SはA, Bを入力とする半加算器の出力\(S_0 = (A\oplus B)\)を1つめの入力とし、2つめの入力にCIとした半加算器の出力であることがわかります。
一方で、桁上げ出力はA, Bを入力とする半加算器の出力と桁上げ入力CIとのAND、さらにその出力を半加算器の桁上げ出力\(C_0 = A\cdot B\)とのOR回路の出力となっていることがわかります。
したがって、全加算器は半加算器2つと、OR回路1つで実現できます。
回路は以下のようになります。
まとめ
本記事では、論理回路で加算する機能を実現するための加算回路を解説しました。加算は、半加算器を組み合わせて全加算器を導出しました。



コメント