本記事では、アクティブノイズコントロール(ANC)の制御方式について説明します。
制御方式
ANCには大きく分けて2つの制御方式が存在します。
- フィードフォワード制御
- 現在の状況を取得せずに、システムのモデルに基づいて動作を予測しながら制御する方式
- フィードバック制御
- 現在の状況を取得しながら、その情報に基づいて制御を行う方式
これら2つを組み合わせたハイブリッド制御も存在します。実システムとしては、ハイブリッド制御が採用されることが多いです。
フィードフォワード制御
フィードフォワード制御の最小構成
フィードフォワード制御方式のANCでは、次の最小限2つの要素が必要となります。
- 騒音源(1次音源)を観測する参照マイクロホン
- 消音するためのスピーカである2次音源
図に示すと以下のようになります。
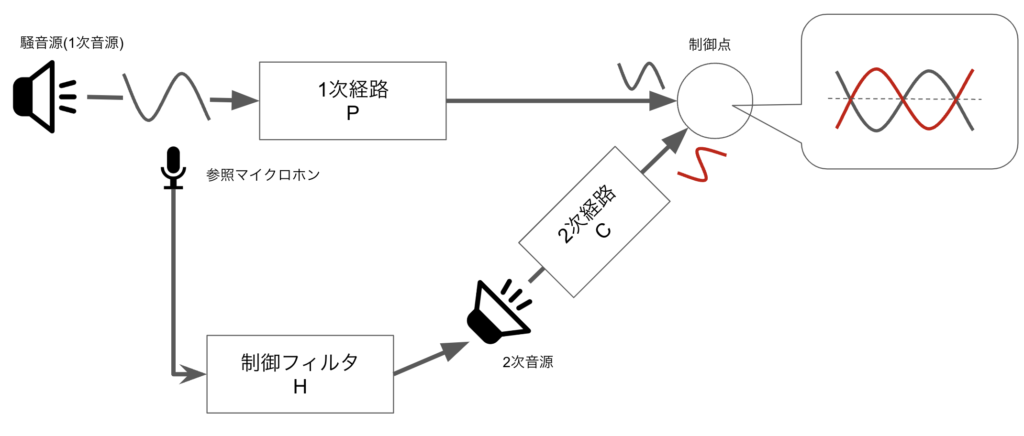
フィードフォワード制御では、1次音源を代表する参照信号を参照マイクロホンにより取得します。この参照信号に基づいて制御フィルタにより信号処理を行い、制御点で逆位相・同振幅となるように制御します。これにより制御点で消音(音圧が0になる)します。
このようにフィードフォワード制御では、参照信号を基にして、「制御点ではこのような波形になっているはず」ということを予測して、「その逆位相・同振幅の音を生成する」手法になります。
フィードフォワード制御の構成
上記に、フィードフォワード制御の最小構成として1個の参照マイクロホン、1個の2次音源が必要であると説明しました。現状の多くのフィードフォワード制御は実際にどの程度音が打ち消されているかを評価するマイクロホンを設置することが基本です。これは誤差マイクロホンと呼ばれます。
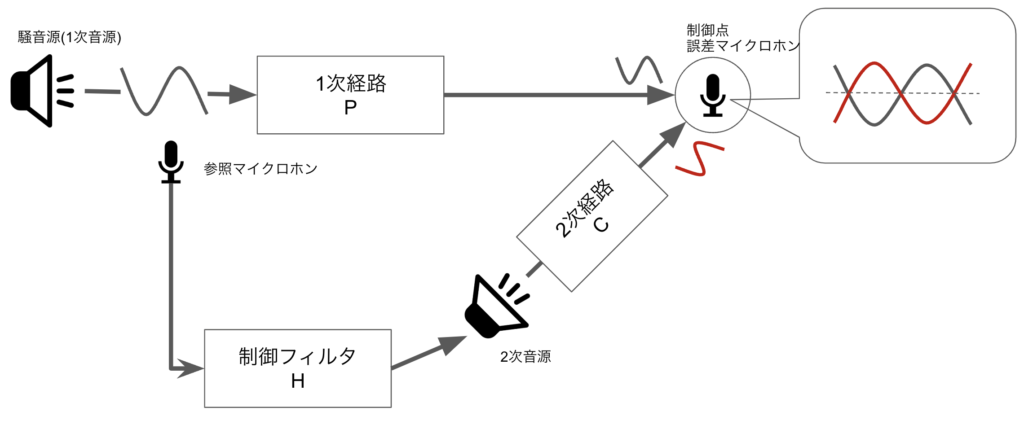
適応アルゴリズムを用いたフィードフォワード制御では、この誤差マイクロホンを利用することが基本となっているため、誤差マイクロホンを加えた3つを最小構成とする場合もあります。
モデル化
上の図をモデル化します。制御点で観測される信号を\(E(\omega)\)とすると、以下のように表されます。
$$E(\omega) = P(\omega) X(\omega) + H(\omega) C(\omega) X(\omega)$$
ここで、\(\omega\)は角周波数を表し、\(X(\omega)\)は参照信号を表します。
また、\(P(\omega)\)は1次音源から制御点までの伝達経路、
\(C(\omega)\)は2次音源から制御点までの伝達経路を表します。
\(H(\omega)\)は制御フィルタにあたり、これをうまく設定することによりANCでは制御点での消音を実現します。
実際には、制御点において音圧が0にしたいため、
$$E(\omega) = 0$$
とすると、
$$H(\omega) = – \frac{P(\omega)}{C(\omega)}$$
が導出できます。したがって、このような制御フィルタを求めることができれば制御点において音圧0が実現できることになります。
フィードフォワード制御を実現させるための条件
フィードフォワード制御では、大きく分けて以下の3つの条件を満たさなければうまく騒音を低減できないことが知られています。
因果律
1つ目は因果律を満たす必要があります。
参照信号が1次経路を経由して制御点に至る時間、と
参照信号を信号処理し、2次音源から放射された音が2次経路を経由して、制御点に至る時間
が一致している必要があります。
1次経路は参照マイクロホンと制御点までの経路なので基本的に固定となり到達するまでの時間は固定となります。
もし信号処理などに時間がかかりすぎると、2次音源から放射される音が制御点に到達する頃には1次音源からの音はすでに通り過ぎてしまうことになります。
したがって、制御が間に合うように処理することを因果律を満たすと言います。
関連度(コヒーレンス)
参照信号と誤差信号の関連度(コヒーレンス)が高いことです。2次音源から放射される制御信号は、参照信号に基づいて信号処理を行い補正を行なったものです。したがって、誤差信号に含まれる参照信号と関連のある成分のみを消音することができます。
2次音源の特性
消音するためには、制御点で1次音源からの音に対して十分余裕を持って大きい2次音源が必要となります。これは消音する周波数帯域すべてで成り立っている必要があります。余裕がない場合は、波形の歪みが発生しやすくなります。
まとめ
本記事では、ANCには2つの制御方式があることを解説しました。また、その中でもフィードフォワード制御の構成について説明しました。

コメント