音声信号処理では,周波数解析手法として離散フーリエ変換(DFT: Discrete Fourier Transform)がよく用いられます.今回はPythonでDFTを実装し、周波数解析を行ってみます.
離散フーリエ変換
音声信号処理では,周波数解析手法として離散フーリエ変換(DFT: Discrete Fourier Transform)がよく用いられます.DFTは次式で定義されます.
$$S(k)=\sum_{t=0}^{N-1}s(t)\exp(-j\frac{2\pi k}{N}t)$$
ここで,\(s(t)\)は\(N\)個の入力をもつ時間領域の信号.
\(j\)は虚数単位.
\(k\)は周波数番号を表しています.
そして,実際の周波数と\(k\)番目の周波数は次のような関係があります.
$$\frac{k}{N} = \frac{F}{F_s}$$
ここで,\(F_s\)はサンプリング周波数を表しています.
この関係は実際の周波数\(F\)[Hz]はサンプリング周波数とデータ数によって決まることを意味しています.
また,周波数領域からの信号を時間領域に戻す逆DFT(Inverse DFT)は次式で定義されます.
$$s(t)=\frac{1}{N}\sum_{t=0}^{N-1}S(k)\exp(-j\frac{2\pi k}{N}t)$$
手順
それでは,定義通りに実装していきます.
dft.pyというファイル名で以下のコードを記述します.
def dft(x):
n = len(x)
X = np.zeros(n,dtype=complex)
for k in range(n):
temp_X = 0
for t in range(n):
A = 2* np.pi * k * t / n
temp_X += x[t] * np.exp(-1j*A)
X[k] = temp_X
return X
def idft(X):
n = len(X)
x = np.zeros(n, dtype=float)
for m in range(n):
temp_x = 0
for t in range(n):
A = 2 * np.pi * m * t / n
temp_x += X[t] * np.exp(1j * A)
x[m] = temp_x / n
return xdftメソッドで,dftを定義し,idftメソッドで逆dftを定義しています.
定義式をそのままnumpyで実装しています.
実行例
今回は音声ファイルを使用するのではなく,わかりやすいようにプログラム上でsin波を合成してDFTを実行します.
fs = 1000 # サンプリング周波数[Hz]
T = 1/fs # サンプリング周期[t]
length = 1000 # 信号の長さ
time = np.arange(0,length)*T # 間
s = 1.0*np.sin(2*np.pi*1*time) + np.sin(2*np.pi*10*time)
plt.plot(s)
plt.show()この信号は1Hzと2Hzのsin波を足し合わせて生成しています.
この信号をプロットすると以下のようになります.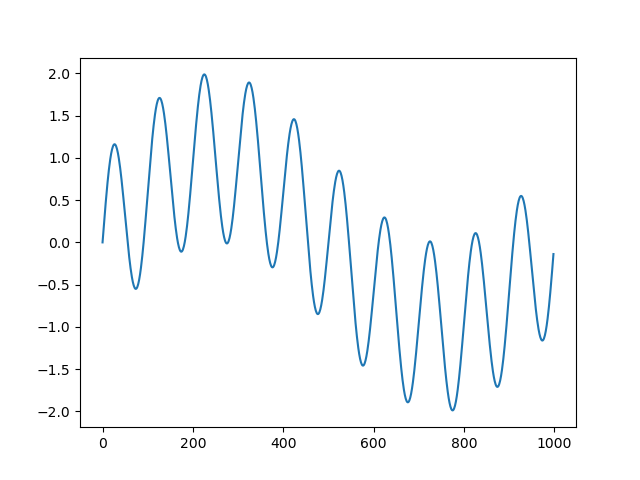
この信号に対してDFTを適用すると以下のようになります.
S = dft(s)
fig, axes = plt.subplots(2)
axes[0].plot(np.abs(S))
axes[1].plot(np.imag(S))
plt.show()ここで,DFTの結果は複素数になるため,実部と虚部に分けてプロットしています.
この図を見ると,共に左右に2つのピークが存在していることがわかると思います.これが1Hz, 2Hzのsin波を表しています.
また,この図を見ると実部,虚部ともに左右対称であることが確認できます.これは,実数信号に対するDFTの結果は実部は偶対称,虚部は寄対称になるという性質があるためです.
上記のように実数信号に対するDFTの結果が左右対称ということは,片側のデータだけで信号の全データを含んでいることになります.そのため,DFTの結果は片側だけ表示することが多いです.
上の図を片側だけ表示し,縦軸,横軸を設定すると以下のようになります.
fs = 1000 # サンプリング周波数[Hz]
T = 1/fs # サンプリング周期[t]
length = 1000 # 信号の長さ
time = np.arange(0,length)*T # 間
frequency = fs*np.arange(0,(length//2))/length
s = 1.0*np.sin(2*np.pi*1*time) + np.sin(2*np.pi*10*time)
S = dft(s)
S2 = abs(S/length)
S1 = S2[:length//2]
plt.plot(frequency, 2*S1)
plt.show()
作成した信号に対して,DFTを実行し,さらに逆DFTを実行すると以下のように元の信号に戻ることが確認できます。
fs = 1000 # サンプリング周波数[Hz]
T = 1/fs # サンプリング周期[t]
length = 1000 # 信号の長さ
time = np.arange(0, length)*T # 間
s = 1.0 * np.sin(2 * np.pi * 1 * time) + np.sin(2 * np.pi * 10 * time)
fig, axes = plt.subplots(4)
axes[0].plot(s)
S = dft(s)
axes[1].plot(np.abs(S))
axes[2].plot(np.imag(S))
axes[3].plot(idft(S))
plt.show()
まとめ
今回は,音声信号処理の基本処理である離散フーリエ変換,逆離散フーリエ変換を実装しました.



コメント