PythonでFIRフィルタを実装する場合、オフライン解析かリアルタイム処理か、信号の長さやタップ長の長さによって最適なメソッドが異なります。それぞれの特徴と実装パターンを整理しました。
オフライン処理の場合
録音済みのデータなど、全てのデータが手元にある場合は、「計算速度」と「位相特性(ズレ)」が重要になります。
ここでは、以下の実装を比較します。
- numpy.convolve
- scipy.signal.convolve
- scipy.signal.lfilter
- scipy.signal.filtfilt
実行結果の比較
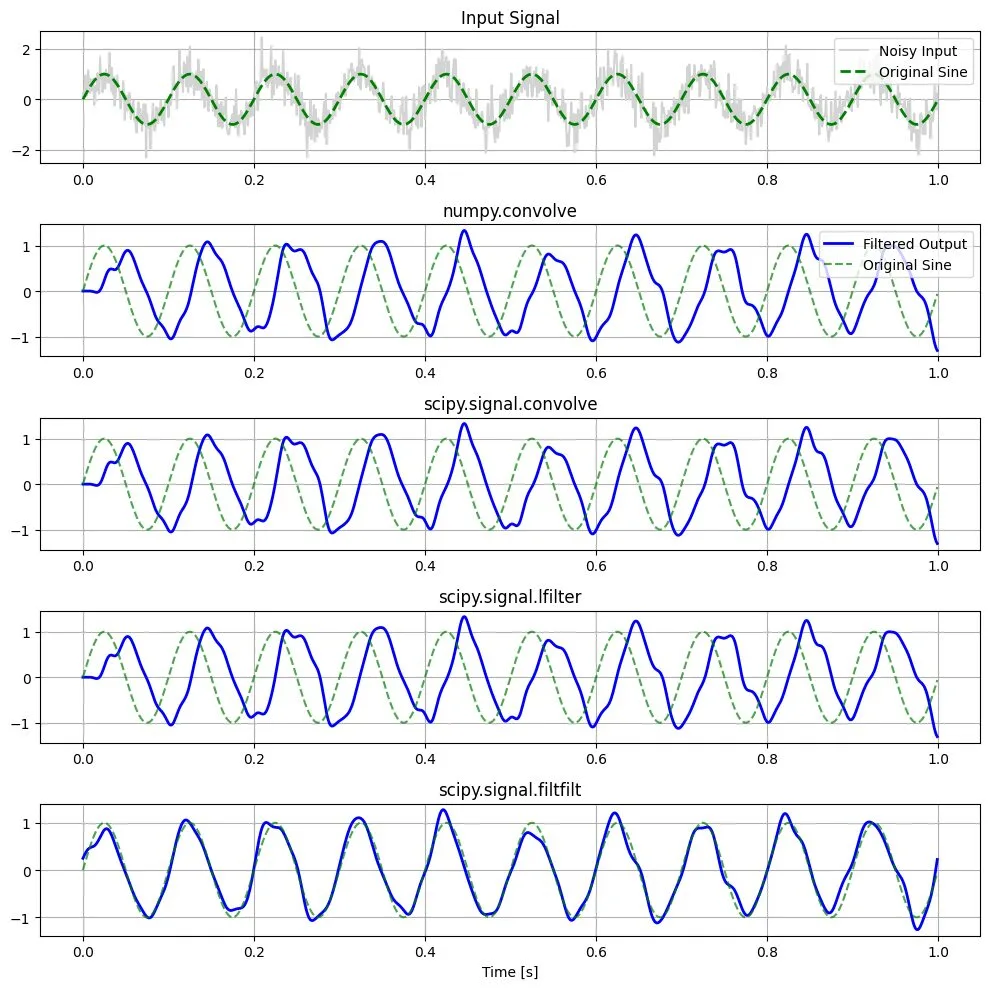
この図を見ると、scipy.signal.filtfiltの結果のみ位相ずれがない結果が得られていることがわかります。位相ずれがないケースの解析結果が欲しい場合は、scipy.signal.filtfiltという結論になります。
import numpy as np
import scipy.signal
import matplotlib.pyplot as plt
#%% --- 1. データ生成 ---
fs = 1000 # サンプリング周波数 (Hz)
duration = 1.0 # 時間 (秒)
t = np.arange(0, duration, 1/fs) # 時間軸
# 信号: 10 Hz の正弦波
freq_signal = 10
clean_signal = np.sin(2 * np.pi * freq_signal * t)
# ノイズ: 白色雑音を加算
np.random.seed(42) # 再現性のため固定
noise = 0.5 * np.random.randn(len(t))
data_stream = clean_signal + noise
#%% --- 2. フィルタ係数の準備 ---
# 10Hzの信号を通し、ノイズをカットするためカットオフを50Hzに設定
numtaps = 51
cutoff_hz = 50
nyquist = 0.5 * fs
b = scipy.signal.firwin(numtaps, cutoff_hz / nyquist)
a = 1.0 # FIRなので分母は1
# %% numpy.convolve
filtered_data_0 = np.convolve(data_stream, b, mode='full')
# %% scipy.signal.convolve
filtered_data_1 = scipy.signal.convolve(data_stream, b, mode='full')
# %% scipy.signal.lfilter
filtered_data_2 = scipy.signal.lfilter(b, a, data_stream)
# %% scipy.signal.lfilter
filtered_data_3 = scipy.signal.filtfilt(b, a, data_stream)
# %%
plt.figure(figsize=(10, 10))
plt.subplot(5, 1, 1)
plt.plot(t, data_stream, label='Noisy Input', color='lightgray', linewidth=1.5)
plt.plot(t, clean_signal, label='Original Sine', color='green', linestyle='--', linewidth=2)
plt.title('Input Signal')
plt.legend(loc='upper right')
plt.grid(True)
plt.subplot(5, 1, 2)
plt.plot(t, filtered_data_0[:len(data_stream)], label='Filtered Output', color='blue', linewidth=2)
plt.plot(t, clean_signal, label='Original Sine', color='green', linestyle='--', linewidth=1.5, alpha=0.7)
plt.title('numpy.convolve')
plt.grid(True)
plt.legend(loc='upper right')
plt.subplot(5, 1, 3)
plt.plot(t, filtered_data_1[:len(data_stream)], label='Filtered Output', color='blue', linewidth=2)
plt.plot(t, clean_signal, label='Original Sine', color='green', linestyle='--', linewidth=1.5, alpha=0.7)
plt.grid(True)
plt.title('scipy.signal.convolve')
plt.subplot(5, 1, 4)
plt.plot(t, filtered_data_2[:len(data_stream)], label='Filtered Output', color='blue', linewidth=2)
plt.plot(t, clean_signal, label='Original Sine', color='green', linestyle='--', linewidth=1.5, alpha=0.7)
plt.grid(True)
plt.title('scipy.signal.lfilter')
plt.subplot(5, 1, 5)
plt.plot(t, filtered_data_3, label='Filtered Output', color='blue', linewidth=2)
plt.plot(t, clean_signal, label='Original Sine', color='green', linestyle='--', linewidth=1.5, alpha=0.7)
plt.grid(True)
plt.title('scipy.signal.filtfilt')
plt.xlabel('Time [s]')
plt.tight_layout()
plt.show()実行時間の比較
次は、実行時間についての比較をしてみます。まずはフィルタ長を固定し、データサイズを可変させた場合の実行時間についてみてみます。
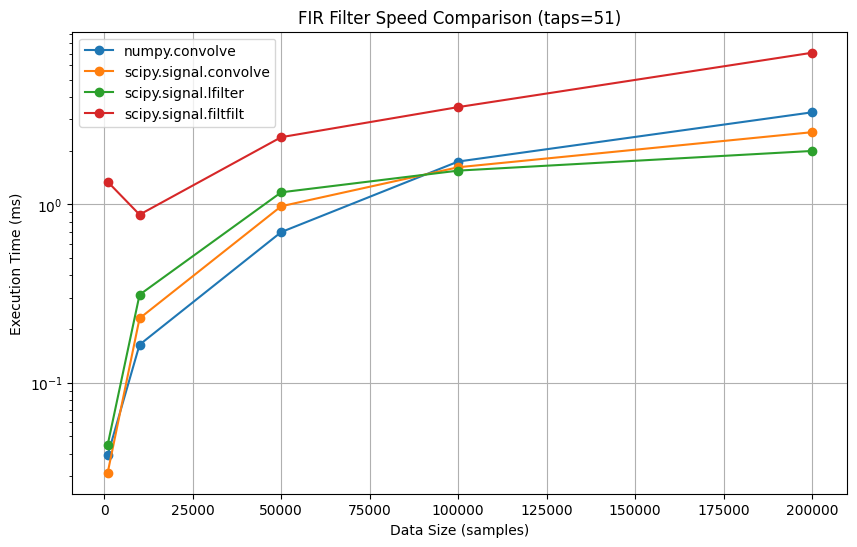
Benchmarking with 51 taps filter...
Data Size | np.conv | sp.conv | lfilter | filtfilt
-----------------------------------------------------------------
1000 | 0.039 | 0.031 | 0.045 | 1.337
10000 | 0.163 | 0.229 | 0.311 | 0.875
50000 | 0.698 | 0.974 | 1.167 | 2.377
100000 | 1.736 | 1.612 | 1.544 | 3.505
200000 | 3.277 | 2.536 | 1.990 | 7.071上記の結果となりました。この結果を見ると、filtfilt以外は大きな差がないことがわかります。
次に、フィルタ長を変えて実行時間を比較してみます。
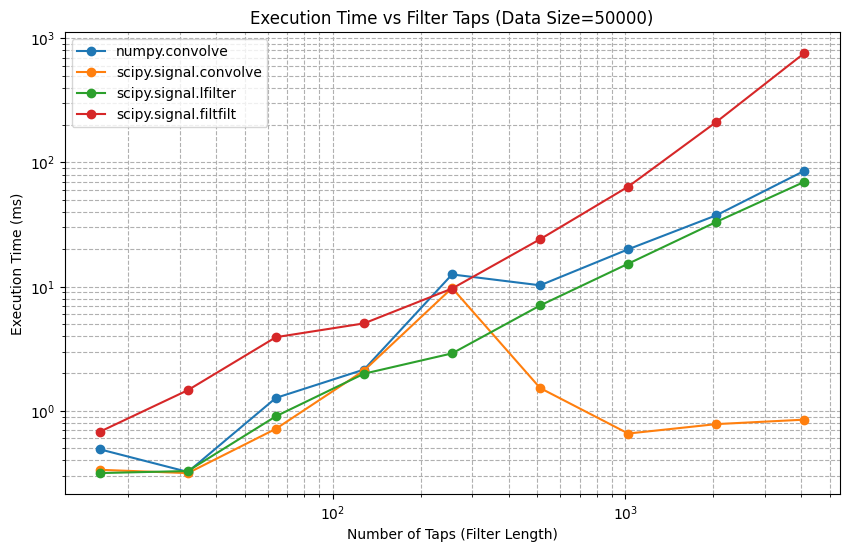
Taps | np.conv | sp.conv | lfilter | filtfilt
-----------------------------------------------------------------
16 | 0.490 | 0.335 | 0.316 | 0.679
32 | 0.322 | 0.315 | 0.328 | 1.468
64 | 1.272 | 0.717 | 0.905 | 3.921
128 | 2.151 | 2.111 | 1.992 | 5.063
256 | 12.549 | 9.762 | 2.903 | 9.659
512 | 10.258 | 1.526 | 7.060 | 24.115
1024 | 20.000 | 0.657 | 15.312 | 63.882
2048 | 37.560 | 0.782 | 33.228 | 211.791
4096 | 85.683 | 0.850 | 69.850 | 759.651この結果を見ると、先ほどと同様にfiltfiltが一番時間がかかっていることがわかります。一方で、scipy.signal.convolveに関して、タップ長をある程度伸ばしたタイミングで急に実行時間が減っていることがわかります。
オフライン処理のまとめ
位相ずれがない解析をしたい場合→ scipy.signal.filtfilt
位相ずれを考慮しない場合 → scipy.signal.convolve
という結論になります。
リアルタイム処理の場合
音声処理やセンサデータのように、データがブロックごとに送られてくる場合、FIRフィルタの内部の遅延器もブロックごとに更新する必要があります。これを行わないと、ブロックの繋ぎ目で不連続点が発生したりしてノイズが発生します。
一つ目の選択肢としては、lfilterです。lfilterは差分方程式を解く関数で、初期状態ziを引数として与えることができます。さらに、戻り値として終了時の状態zfを返すため、これを使用することで連続的な処理が可能です。
二つ目の選択肢は自作です。上記の結果から、タップ長が大きい場合、単純なオフラインのFIRフィルタはscipy.signal.convolveが一番速いという結果になりました。つまり、scipy.signal.convolveを使い、遅延器の更新は自分でするという方針になります。
import numpy as np
from scipy import signal
import timeit
# lfilter
def lfilter_test():
# 1. フィルタ係数の準備
numtaps = 512
b = signal.firwin(numtaps, cutoff=0.1)
a = 1.0 # FIRなので分母は1
# 2. 初期状態(zi)の作成
# フィルタの状態変数のサイズは len(b) - 1
zi = signal.lfilter_zi(b, a) * 0 # 最初はゼロ初期化
# ストリーミング処理の模倣(ブロックごとに処理)
block_size = 1024
# data_stream は長い音声データなどと仮定
data_stream = np.random.randn(10000)
processed_blocks = []
for i in range(0, len(data_stream), block_size):
# 現在のブロックを取得
block = data_stream[i : i + block_size]
# フィルタ適用
# zi: 前回の状態, zf: 今回の終了状態
out_block, zf = signal.lfilter(b, a, block, zi=zi)
# 次のループのために状態を更新
zi = zf
processed_blocks.append(out_block)
result = np.concatenate(processed_blocks)
# fir 自作
def fir_test():
# 1. フィルタ係数の準備
numtaps = 512
b = signal.firwin(numtaps, cutoff=0.1)
input_buffer = np.zeros(numtaps - 1)
block_size = 1024
data_stream = np.random.randn(10000)
processed_blocks = []
for i in range(0, len(data_stream), block_size):
# 現在のブロックを取得
block = data_stream[i : i + block_size]
input_chunk = np.concatenate((input_buffer, block))
out_block = signal.convolve(input_chunk, b, mode='valid', method='auto')
input_buffer = block[-(numtaps - 1):]
processed_blocks.append(out_block)
result = np.concatenate(processed_blocks)
t0 = timeit.timeit(lfilter_test, number=num_loops)
t1 = timeit.timeit(fir_test, number=num_loops)
print(f"lfilter: {t0 / num_loops}")
print(f"fir self: {t1 / num_loops}")結果は以下のようになりました。
lfilter: 0.009307412500493228
fir self: 0.0021318228915333747このため、基本的には自作した方が高速になります。
まとめ
オフライン処理の場合、
- 位相ずれをなくしたい場合→ filtfilt
- 位相ずれはそのままでいい場合→ sicpy.signal.convolve
リアルタイム処理の場合はオフライン結果より、sicpy.signal.convolveが一番高速となるので、これを利用した自作が高速になる。ただし、実装が面倒なのでlfilterを使う方が楽な場合もある。




コメント