xを説明変数、yを目的変数と呼びます。説明変数が1つの場合は単回帰、2つ以上の場合は重回帰と呼びます。
単回帰:
$$y = w_0 + w_1 x$$
重回帰:
$$y = w_0 + w_1 x_1 + w_2 x_2 + \cdots + w_m x_m$$
LinearRegressionの使い方
【LinearRegression()の引数】
- fit_intercept:Falseの場合、切片を求める計算を含まない(デフォルトはTrue)
- normalize:Trueの場合、説明変数を正規化する(デフォルトはFalse)バージョン1.0以降廃止
- copy_X: メモリ内でデータを複製するか(デフォルトはTrue)
- n_jobs: 計算に使うジョブの数、-1 に設定すると、すべての CPU を使って計算(デフォルトは1)
- positive: 係数を強制的に正の値のみにする(デフォルトはFalse)
また、作成したインスタンスへの基本的なメソッドは以下となります。【sklearn.linear_model.LinearRegressionクラスのメソッド】
fit(X, y[, sample_weight]):学習の実行get_params([deep]):学習の際に用いたパラメータの取得predict(X): 予測の実行score(X, y[, sample_weight]): 決定係数の算出set_params(**params): パラメータの設定
ライブラリのインポート
import pandas as pd
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import matplotlib.pyplot as pltデータセットの準備
diabetes_df = load_diabetes(as_frame=True).frame学習用とテスト用にデータを分割
学習データを0.7, テスト用データを0.3の割合でデータを分割します。
X = diabetes_df['bmi'].values.reshape(-1, 1)
y = diabetes_df["target"].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42,
)単回帰分析
モデルの構築と学習
単回帰分析では、説明変数が一つなので、特徴量が一つになります。ただし、APIの使用としてモデルの説明変数は二次元を渡す必要があるため、Xは二次元にすることに注意してください。
model = LinearRegression(
fit_intercept=True,
copy_X=True,
n_jobs=1,
positive=False,
)
model.fit(X_train, y_train)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)評価と可視化
青色の点が学習データ、オレンジ色の点がテストデータを表しています。赤が線形回帰モデルによって求めた回帰直線になります。
plt.scatter(X_train, y_train, label="train")
plt.scatter(X_test, y_test, label="test")
plt.plot(X_test, y_test_pred, color = "red", label="regression line")
plt.legend()
plt.show()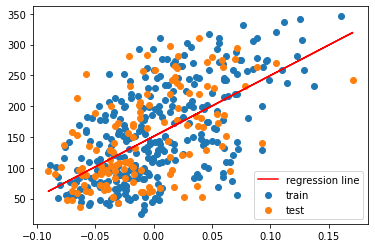
回帰の評価には、残差プロットと呼ばれるものが使用されることがあります。横軸に予測値をとり、縦軸に残差(予測誤差)をとって、プロットしたものになります。視覚的に確認することができるので、何らかの規則性やばらつきなどを判断することができます。
figure, axes = plt.subplots(1, 2, figsize=(20,5))
axes[0].scatter(y_train_pred, y_train_pred - y_train)
axes[0].hlines(y=0, xmin=np.min(y_train_pred), xmax=np.max(y_train_pred))
axes[1].scatter(y_test_pred, y_test_pred - y_test)
axes[1].hlines(y=0, xmin=np.min(y_test_pred), xmax=np.max(y_test_pred))
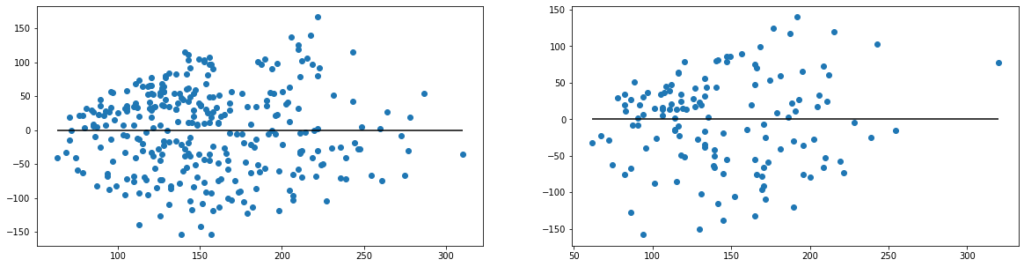
回帰問題の評価指標として一般的に使用されるMAE(Mean Absolute Error)、決定係数(Coefficient of determination、\(R^2\))で評価します。
print("MAE train data: ", mean_absolute_error(y_train, y_train_pred))
print("MAE test data: ", mean_absolute_error(y_test, y_test_pred))
print("R2 train data: ", r2_score(y_train, y_train_pred))
print("R2 test data: ", r2_score(y_test, y_test_pred))MAE train data: 51.95119946335585
MAE train data: 50.593075043758716
R2 train data: 0.3657651200418852
R2 test data: 0.2803417492440603重回帰分析
重回帰分析では、説明変数が複数あります。従って、Xが多次元の特徴量になりますが、基本的な進め方は単回帰分析と同じです。
モデルの構築と学習
X = diabetes_df[['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']].values
y = diabetes_df["target"].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42,
)
model = LinearRegression(
fit_intercept=True,
copy_X=True,
n_jobs=1,
positive=False,
)
model.fit(X_train, y_train)評価と可視化
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
figure, axes = plt.subplots(1, 2, figsize=(20,5))
axes[0].scatter(y_train_pred, y_train_pred - y_train)
axes[0].hlines(y=0, xmin=np.min(y_train_pred), xmax=np.max(y_train_pred))
axes[1].scatter(y_test_pred, y_test_pred - y_test)
axes[1].hlines(y=0, xmin=np.min(y_test_pred), xmax=np.max(y_test_pred))
print("MAE train data: ", mean_absolute_error(y_train, y_train_pred))
print("MAE train data: ", mean_absolute_error(y_test, y_test_pred))
print("R2 train data: ", r2_score(y_train, y_train_pred))
print("R2 test data: ", r2_score(y_test, y_test_pred))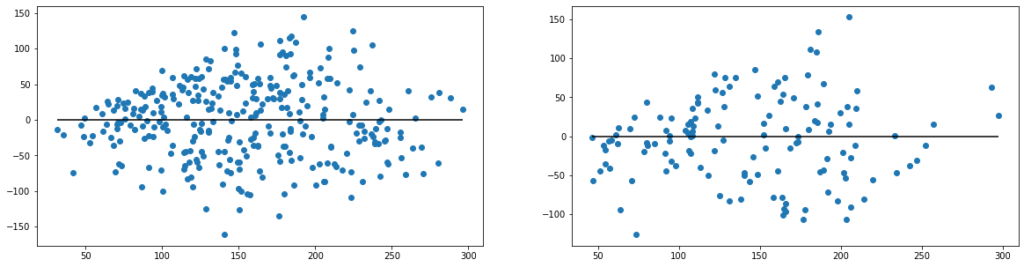
MAE train data: 44.09784735010516
MAE train data: 41.9192536055668
R2 train data: 0.524413200822697
R2 test data: 0.4772920174157329まとめ
本記事では、scikit-learnを用いて線形回帰モデルを構築する手順を解説しました。単回帰分析と重回帰分析では同じLinearRegressionモデルを使用することで同様に使用することができます。



コメント