私たちの身の回りは波で溢れています。例えば、池に石を投げたときに水面を伝わるのも波です。水面が上下に振動しながら、その揺れが周囲に伝わっていく現象です。
はじめに
私たちの身の回りは波で溢れています。
例えば、池に石を投げたときに水面を伝わる波。あれは水面が上下に振動しながら、その揺れが周囲に伝わっていく現象です。
音も空気が圧縮と膨張という振動を繰り返して伝わっているからです。
波の式
この波という現象を数式で表すと、三角関数（サイン・コサイン）で表されます。
$$y(t) = A \sin 2\pi f t$$
高校数学では、三角関数といえば、直角三角形の辺の比率として定義されていました。一見関係なさそうな三角関数と波が水や空気の振動につながるのかについて解説していきます。
三角関数
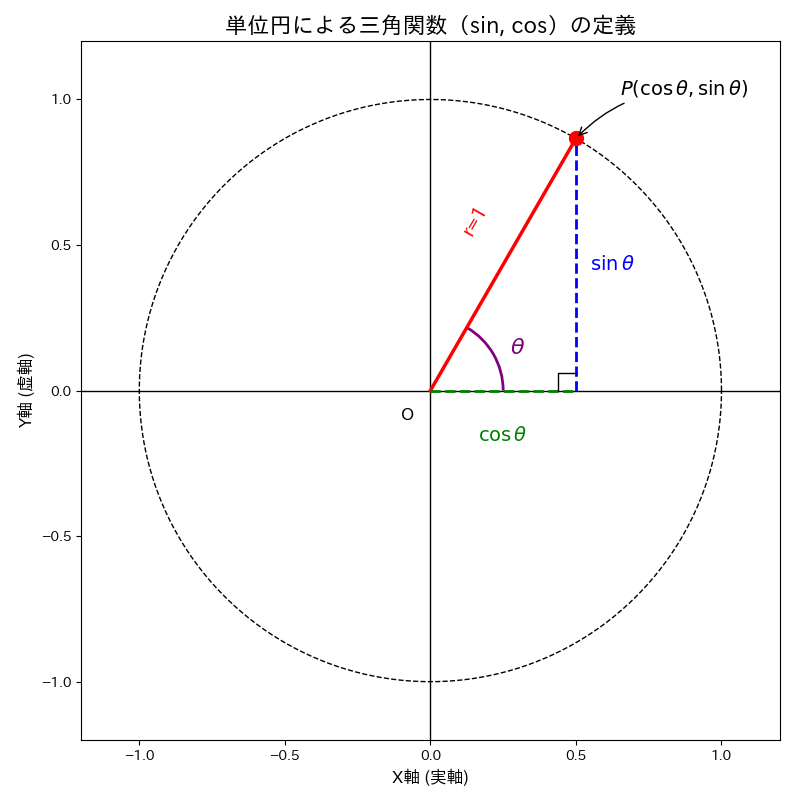
まずは高校数学で習った、sin, cosの定義を再確認しましょう。三角関数を定義するとき、単位円を利用します。単位円というのは半径が1の円で、この単位円の円周上の座標を利用して三角関数を定義します。
単位円上に点P(x, y)をとります。このPに向かって原点から線を結びます。また、この点Pからx軸に向かって垂直に線を下ろすと直角三角形ができます。
このときの角度を\(\theta\)とすると、
$$\sin \theta = y$$
$$\cos \theta = x$$
$$\tan \theta = \frac{y}{x}$$
正弦波
上記の定義より、\(y = sin\theta \)と表されることがわかりました。少し最初の式の形に似ています。
ここで、先ほどの円周上の点Pが一定のスピードで回ることを考えてみます。
$\theta$（角度）は単なる「位置」を表します。これを動的な動きにするために、角速度 $\omega$（オメガ）を導入します。
角速度 \(\omega\) は「1秒間に何度進むか」というスピードです。
これに経過時間 $t$ を掛けると、その時の角度 \(\theta\) になります。
$$\theta = \omega t$$
これを代入すると、時間に依存する関数になります。
$$y(t) = \sin(\omega t)$$
これをアニメーション化したのが以下です。
動画を見ると、左側では点が円の上をぐるぐると一定の速さで回っています。
ここで、この赤い点の高さだけに注目してみましょう。点は上がったり下がったりを繰り返していますね。これこそが、最も純粋な振動の形です。
この高さの変化を、時間を横軸にして記録していくと右側に波の形が現れることがわかります。
物理の世界では「1秒間に何度進むか（角速度）」よりも、「1秒間に何回転するか（周波数 $f$）」の方が直感的です。2回転する例が以下です。
1回転は \(2\pi\) です。1秒間に\(f\) 回転するということは、角度は \(2\pi f\)進むということになります。
つまり、
$$\omega = 2\pi f$$
という関係が成り立ちます。
これを式に入れると、よく見る形に近づきます。
$$y(t) = \sin 2 \pi f t$$
最後に、波の大きさを調整します。
sin の値は必ず単位円を考えているので、-1から+1 の範囲に収まりますが、実際の音や電気の波はもっと大きかったり小さかったりします。そこで、最大値を決める係数A振幅を掛けます。
$$y(t) = A \sin(2\pi f t)$$
最初に提示した波の式になりました。
余談
今回は波に三角関数との関係性を天下り的に説明しました。
三角関数はもともと、古代ギリシャの時代に天文学と測量のために生まれました。
三角関数は、
- 円
- 角度
- 長さ
を扱うための幾何学ツールでした。
17世紀になると、
- 運動
- 振動
- 微分積分
が登場します。
ここで重要人物がアイザック・ニュートンとゴットフリート・ライプニッツです。
彼らが微分積分を作ったことで、
$$y(t) = \sin \omega t$$
のように、ここで初めて、三角関数が動くようになります。
次に重要なのが18世紀の解析力学です。
弦の振動問題を研究したジャン・ル・ロン・ダランベールやレオンハルト・オイラーは、弦の振動を次のような方程式で表しました。
$$\frac{d^2x}{dt^2} + \omega^2 x = 0$$
これを解くとどうなるか？
$$x(t) = A \sin \omega t + B cos \omega t$$
ここで、振動・波は三角関数で表現できるんだということが理解されます。
この式がどのように導出されるのかは以下の記事で解説しています。
まとめ
本記事では、三角関数と波の関係性について解説しました。
コメント