単振動

単振動

高校物理では、単振動は波として表現できる、ということを習ったかと思います。そのことについてなぜそうなるのかを解いていきます。

モデル化

まずは単振動という現象を数式としてモデル化することから始めます。

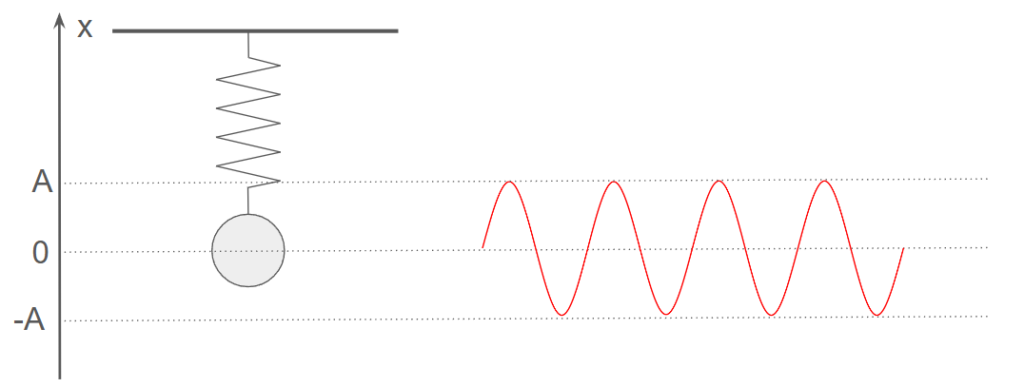
図に示すように、ばねにおもりをつるすと、バネが伸びて静止します。このように、力が釣り合い静止した状態を平衡状態といいます。

この平衡状態でのおもりの位置から少し引っ張って下げ、そっと手を放すとばねが伸び縮みして、振動をはじめます。

平衡状態でのおもりの位置をx=0とすると、伸び縮みして平衡状態からおもりの位置が変化します。この位置の変化を変位といい、このとき、おもりにかかる力はフックの法則を用いて次式で表されます。

$$F=-kx$$

ここで、比例係数k[N/m]はバネの硬さを表す量で、ばね定数と呼ばれます。

ここで、負の値となっているのは、おもりの変位と逆方向に力が働いているからです。

ばねが伸びたとき、つまり、x < 0 のときにはばねを縮ませようとする力が働き、ばねが縮んだときは、x > 0 のときには、ばねを伸ばそうとする力が働きます。

このように、平衡状態の位置から離れると、平衡状態に戻そうとする力を復元力といいます。この力の働きがくりかえ起こることでばねが振動を続けることになります。

運動方程式を解く

おもにについてニュートンの運動方程式は次式であらわされます。

$$ma=F$$

ここで、m[kg]はおもりの質量、a[m/s^2]は加速度, Fは力を表します。

これに先ほど求めた力を代入すると、次のようになります。

$$m \frac{d^2 x}{dt^2} = -k x$$

ここで、加速度aは変位xについての２階微分のため、このように表しています。

この式を解くことで、単振動の式を得ることができます。

この式は、2階同次微分方程式と呼ばれる形になっていますので、これを解けばよいということになります。この形式の微分方程式の詳しい解法は別記事にしますが、2階同次微分方程式の解となる式は、2つ存在し（特殊解とよぶ）、これらの式の線形結合が解となる式（一般解）となることが知られています。

この2階同次方程式の解放は特性方程式を立てることで求めることが知られています。

まず、解となる式を一旦\(x = e^{\lambda t}\)となるとします。これを先ほどの式に代入すると、

$$m (e^{\lambda t}\ )’’ = -k x $$

$$m \lambda^2 (e^{\lambda t}\ ) + k (e^{\lambda t}\ ) = 0$$

$$(e^{\lambda t}\ ) (m \lambda^2 + k) = 0$$

したがって、

$$m \lambda^2 – k = 0$$

を解けばいい、したがって、

$$ \lambda^2 = – \frac{k}{m}$$

$$ \lambda = \pm \sqrt{- \frac{k}{m}}$$

$$\lambda = \pm i\omega $$

ここで、\(\omega=\sqrt{\frac{k}{m}}\)とおく。

2階同次微分方程式の解は2つの一般解の線形結合により求められるため、解は次のようになります。

$$x = c_1 e^{i \omega t} + c_2 e^{-i \omega t}$$

これで、解が求まりました。しかし、複素数が出ているためもう少し整理します。

ここで、オイラーの公式を利用します。

$$ e^{i\theta} = cos \theta + i sin \theta$$

これを利用すると、次のようになります。

$$c_1(cos \omega t + i sin\omega t) + c_2(cos \omega t – i sin \omega t)$$

$$= (c_1 + c_2) cos \omega t + i (c_1 – c_2) sin \omega t $$

ここで、xは実数のため、iをうまく消す必要があります。ここで、\(c_1, c_2\)はそれぞれ複素素数の任意定数であることに注意します。したがって、\(c_1, c_2\)はそれぞれ次のように表されます。

$$c_1 = a_1 + b_1 i$$

$$c_2 = a_2 + b_2 i $$

ここで、\(a_1, a_2, b_1, b_2\)はそれぞれ実数です。これらをさらに代入すると、次のようになります。

$$(a_1 + b_1 i + a_2+ b_2 i )cos\omega t + i(a_1 + b_1i – a_2 – b_2i)sin \omega t$$

$$= (a_1 + a_2) cos\omega t + (b_1 – b_2) sin \omega t + (b_1 + b_2) i cos \omega t + (a_1 – a_2) i sin \omega t$$

したがって、\(a_1 – a_2 = 0\), \(b_1+b_2 = 0\) となり、

$$2 a_1 cos\omega + 2 b_1 sin\omega $$

という解が得られます。これを三角関数の合成を用いて、整理すると

$$2\sqrt{a_1^2 + b_1^2} sin(\omega t + \alpha)$$

$$tan\alpha = – \frac{a_1}{b_1}$$

となります。これをさらに\(A = 2 \sqrt{a_1^2 + b_1^2}\)とすると、

$$x = Asin(\omega t + \alpha)$$

となり、高校物理で公式として出ていた単振動の式が導出されました。

このように、おもりの位置は三角関数で表される、周期的な変化をすることがわかります。このような運動を単振動あるいは調和振動と呼びます。

周期

三角関数の周期性により、2πの位相が変化すると元の状態にもどる。このとき、時刻tからT秒経過したとすると、次の等式が成り立つ。

$$\omega (t + T) + \alpha= \omega t + \alpha + 2\pi$$

この式を、Tについて解くと、

$$T= 2\pi \frac{1}{\omega} = 2\pi \sqrt{\frac{m}{k}}$$

このTを単振動の周期という。この式から、おもりが軽い(mが小さい)ほど、あるいはばねが硬い(kが大きい)ほど、短い周期で振動することがわかります。

ここで、周期の逆数をとった

$$f = \frac{1}{T} = \frac{\omega}{2\pi}$$

を周波数という。また、\(\omega\)は角周波数という。

特に、この角周波数および周波数は、ばね定数（復元力を表すパラメータ）とおもりの質量（慣性力を表すパラメータ）だけで決まる値なので、とくに固有（角）振動数とよぶ。

固有振動数は、おもりを振動させるために最初に引っ張った変位量や重力の大きさに依存せず、ばねとおもりの特性だけで決まるあたいとなります。