ディジタルフィルタの構成要素
前回の記事の線形差分方程式からわかるようにディジタルフィルタは以下の3つの要素から構成されます。
- 遅延器(ディレイ)
- 加算器
- 乗算器
これらの構成要素を用いれば、\(N\)次の線形差分方程式で記述されるディジタルフィルタは下図のようなブロック図で表されます。
| 構成要素 | 式 | ブロック図 |
| 遅延器 | $$y[n] = x[n-1]$$ | 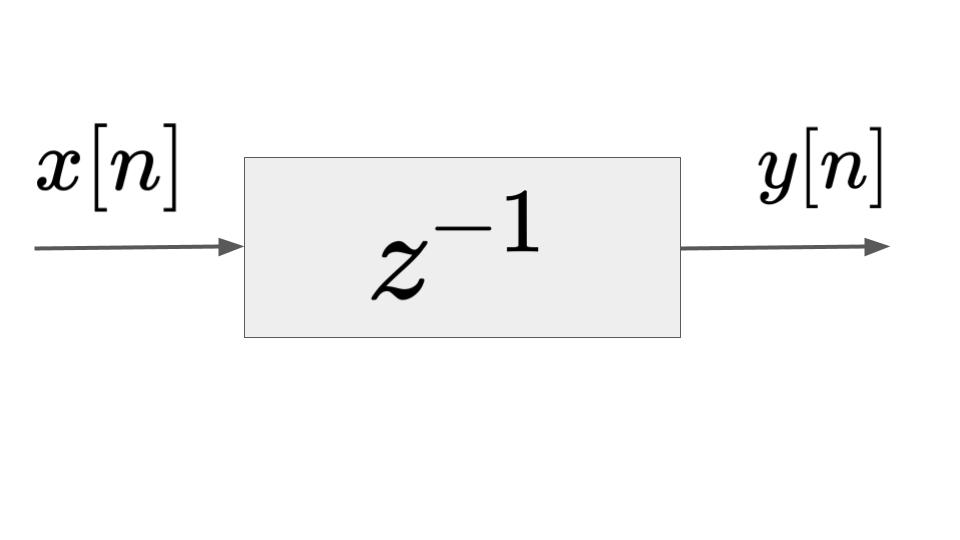 |
| 加算器 | $$y[n] = x_1[n] + x_2[n]$$ | 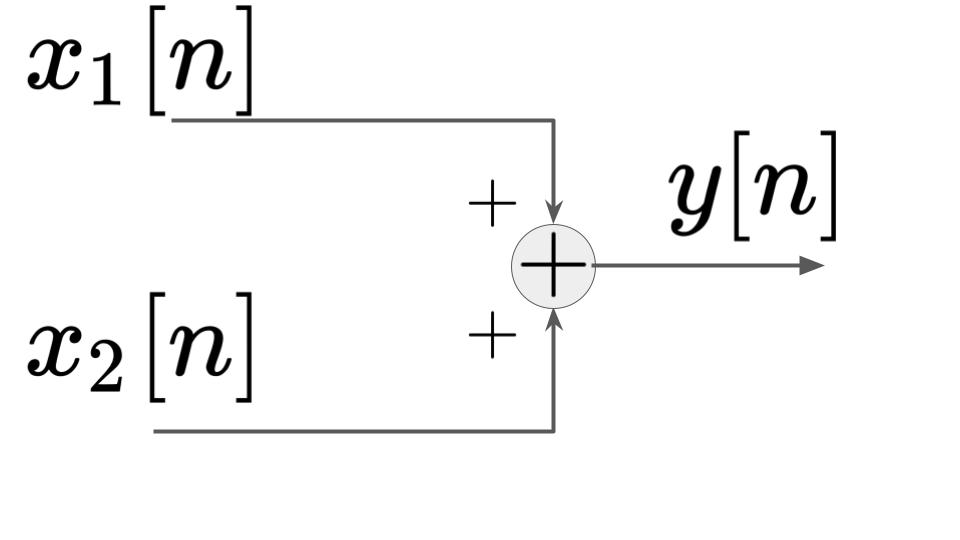 |
| 乗算器 | $$y[n] = ax[n]$$ | 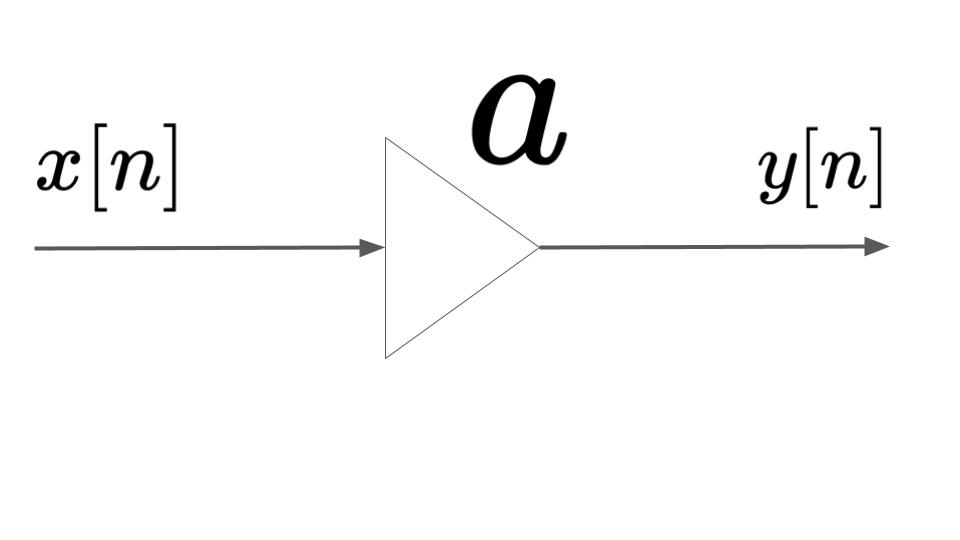 |
ディジタルフィルタの回路構成
ディジタルフィルタの回路構成は4パターンあります。
- 直接型Ⅰ(Direct from Ⅰ)
- 直接型Ⅱ(Direct from Ⅱ)
- 転置直接型Ⅰ(Transposed Direct from Ⅰ)
- 転置直接型Ⅱ(Transposed Direct from Ⅱ)
次の差分方程式で表されるディジタルフィルタを考えます。
$$y[n] = \sum_{i=0}^{N=2} b_i x[n-i] – \sum_{j=1}^{N=2} a_i y[n-j]$$
直接型Ⅰ(Direct formⅠ)
直接型Ⅰは、上記の式をそのままに構成した回路構成のため、直接型Ⅰと呼ばれます。この場合、必要とする遅延器の数は\(2N\)個です。これは差分方程式の次数あるいはフィルタの次数\(N\)の2倍です。上記の直接型Ⅰの回路構成は下図のようになります。
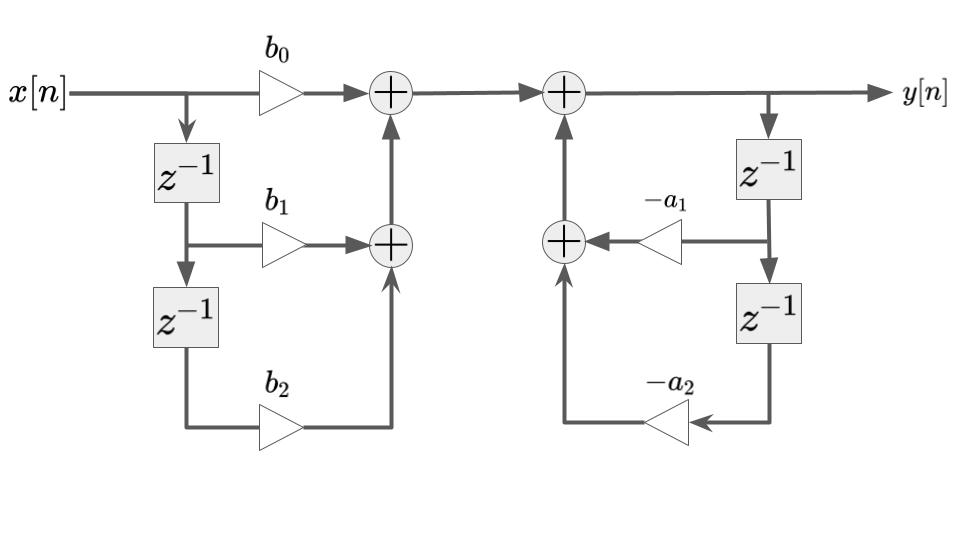
直接型Ⅱ(Direct form Ⅱ)
直接型Ⅰのディジタルフィルタは、2つのフィルタが縦続接続されたものと考えることができます。ディジタルフィルタの縦続接続は順番を変更しても、入出力特性は変わらないため、直接型Ⅰのフィルタは下図のように変更できます。このようなフィードバック部分とフィードフォワード部分の構成を入れ替えたものを直接型Ⅱと呼びます。
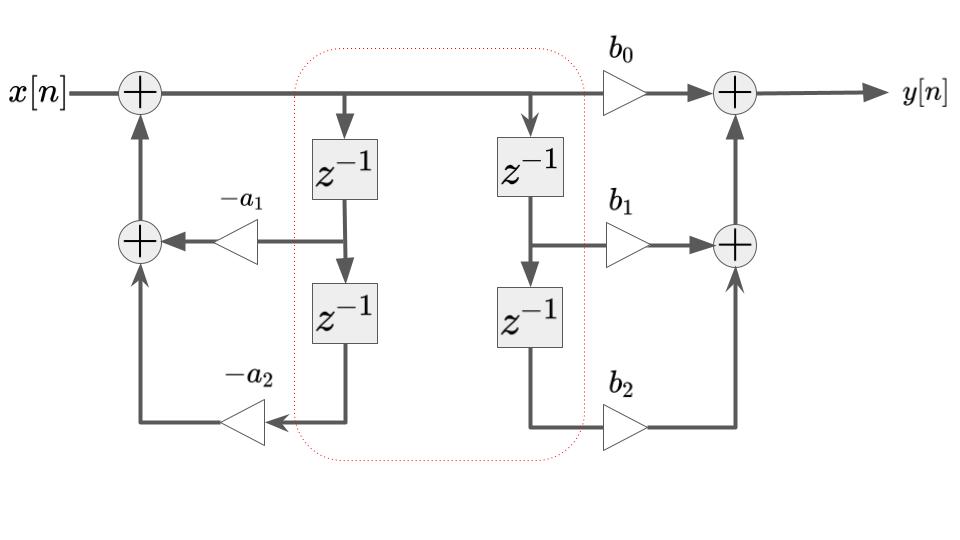
ここで、真ん中の遅延器のそれぞれの入力および出力は同じなので、同じ遅延器を共有して使うことができます。共有した遅延器を用いて表すと下図のようになります。この場合、必要となる遅延器の数はディジタルフィルタの次数\(N\)と等しいです。
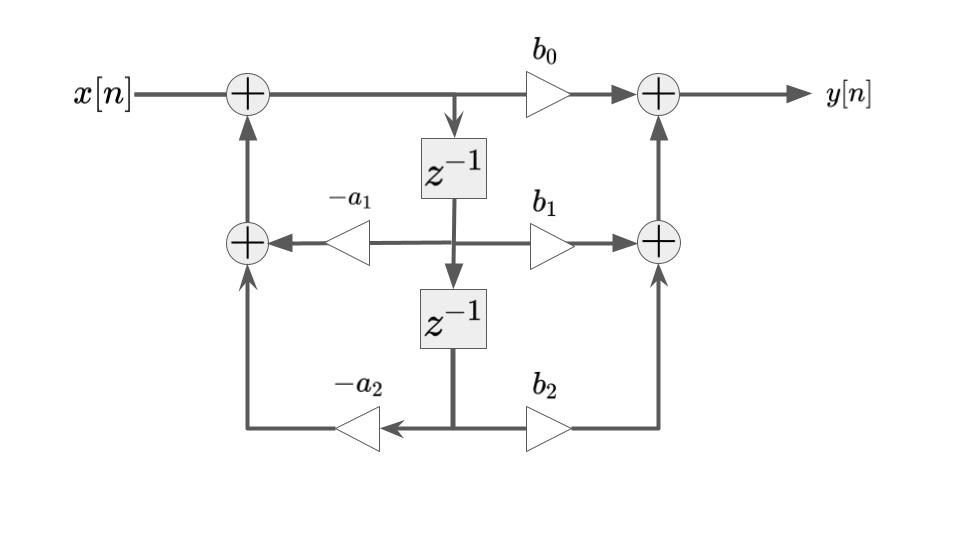
直接型Ⅱに限らず、遅延器の数とディジタルフィルタの次数\(N\)が等しい場合、標準型(Canonic form)と呼びます。
転置型
残り2つのタイプの構成は、上記の2つのタイプを転置することで得られます。転置は以下の操作により行います。
- 信号の流れをすべて逆転する
- 加算器と分岐点を交換する
- 入力と出力を交換する(信号図として反転させる)
上記の直接型Ⅰを転置すると、下図が得られます。
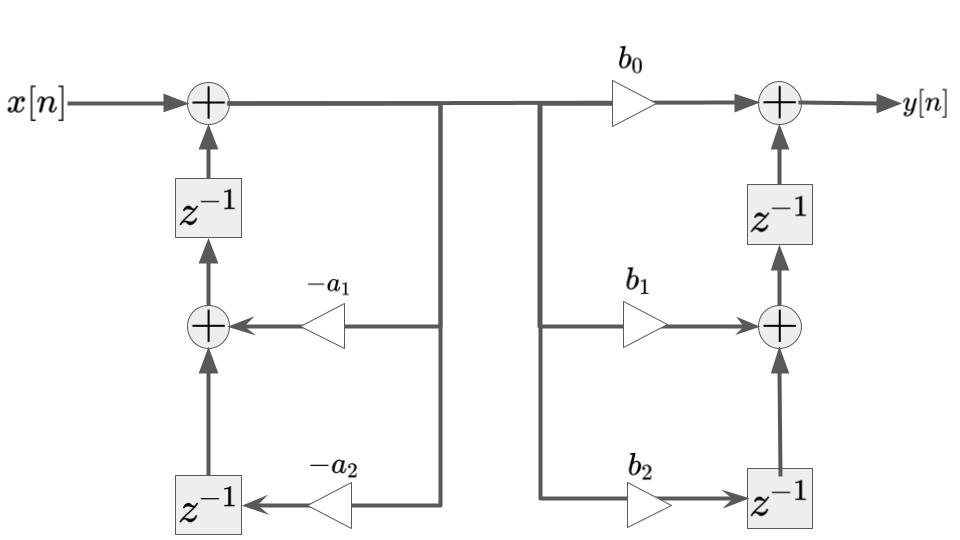
次に直接型Ⅱを転置すると、下図が得られます。
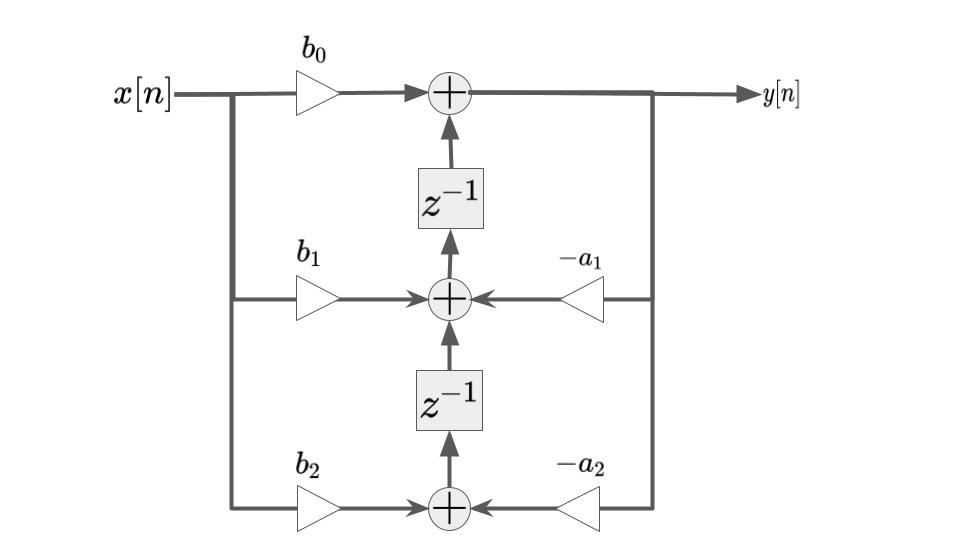



コメント