本記事では、ディジタル信号処理でよく使用される基本的な信号をPythonを用いて生成し、図示したいと思います。
基本的な信号
単位インパルス
単位インパルス信号は、クロネッカーのデルタ関数とも呼ばれ、アナログの信号処理や制御システム理論で用いられる、ディラックのディラク関数と同じ役割を持ちます。
従って、システムの応答を知るために非常に重要な信号となります。
単位インパルス信号は次式で表されます。
$$x[n] = \begin{cases} 1 & n=0 \\ 0 & n \neq 0 \end{cases}$$
式より、ある1サンプルのみが、1となり、そのほかの信号は全て0となるような信号であることがわかります。
単位ステップ
単位ステップ信号は、あるサンプル以降は全て1のような信号です。
単位ステップ信号は、次式で表されます。
$$x[n] = \begin{cases} 1 & n\geq0 \\ 0 & n < 0 \end{cases}$$
別の表し方として、インパルス応答を使用して単位ステップ信号を表してみます。
$$x[n] = \sum_{k=0}^{\infty}\delta[n-k]$$
ここで、\(\delta[n]\)はインパルス信号を表しています。このように、ステップ信号は時間的に推移した(サンプルをずらす)単位インパルスの無限和としてあらわすことができます。
このことは、畳み込みなどの概念を理解するために非常に重要です。
ランプ信号
ランプ信号は、あるサンプル以降は傾き1の直線となる信号です。
ランプ信号は、次式で表されます。
$$x[n] = \begin{cases} n & n\geq0 \\ 0 & n < 0 \end{cases}$$
ランプ信号は、ディープラーニングの活性化関数としてもよく使用されており、その場合ReLu関数と呼ばれています。
その場合は、以下のような定義式もよく見られます。
$$x[n] = max(n, 0)$$
先ほど、単位ステップ信号がインパルス信号で表すことができることを説明しましたが、このランプ信号はステップ信号で表すことができます。ステップ信号を用いて表すことができるということは、インパルス信号でも表すことができます。
次式のようにステップ信号を用いてランプ信号を表してみます。
$$x[n] = n u[n]$$
ここで、\(u[n]\)はステップ信号を表しています。
ステップ信号はインパルス信号の時間的に推移した無限和で表すことができ、ランプ信号はステップ信号に係数をかけることで表すことができます。
指数関数
指数関数は、次式で定義されます。
$$x[n] = \begin{cases} \alpha^n & n\geq0 \\ 0 & n < 0 \end{cases}$$
この指数関数信号もステップ信号を用いて表すことができます。
$$x[n] = \alpha^n u[n]$$
基本的な信号の生成
上記のディジタル信号処理において、基本的な信号を生成するPythonプログラムを以下に示します。
import matplotlib.pyplot as plt
import numpy as np
def impulse(x):
return np.where(x == 0, 1, 0)
def step(x):
return 1 * (x > 0)
def ramp(x):
return np.maximum(x, 0)
def exponential(alpha, x):
return np.where(x > 0, alpha**x, 0)
def step_2(x):
k = x[x >= 0]
y = np.zeros(len(x))
for k_i in k.tolist():
y += impulse(x - k_i)
return y
def ramp_2(x):
return x * step(x)
def exponential_2(alpha, x):
return (alpha**x) * step(x)
def main():
n = np.arange(-20, 20)
x1 = impulse(n)
x2 = step(n)
x3 = ramp(n)
x4 = exponential(0.8, n)
fig, axes = plt.subplots(4, 1, figsize=(10, 15))
axes[0].stem(n, x1)
axes[0].set_title("impulse function")
axes[1].stem(n, x2)
axes[1].set_title("step function")
axes[2].stem(n, x3)
axes[2].set_title("ramp function")
axes[3].stem(n, x4)
axes[3].set_title("exponential function")
x1 = impulse(n)
x2 = step_2(n)
x3 = ramp_2(n)
x4 = exponential_2(0.8, n)
fig2, axes2 = plt.subplots(4, 1, figsize=(10, 15))
axes2[0].stem(n, x1)
axes2[0].set_title("impulse function")
axes2[1].stem(n, x2)
axes2[1].set_title("step function")
axes2[2].stem(n, x3)
axes2[2].set_title("ramp function")
axes2[3].stem(n, x4)
axes2[3].set_title("exponential function")
if __name__ == "__main__":
main()
実行結果
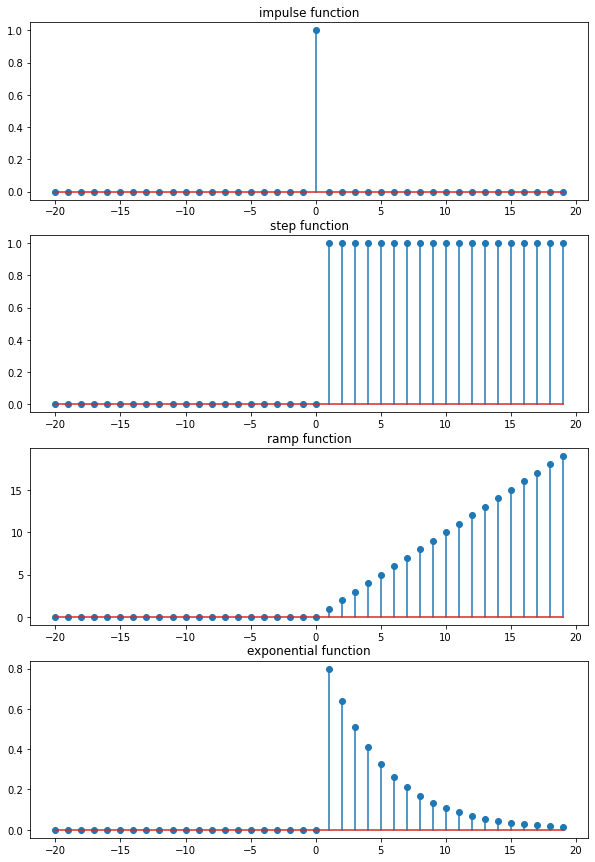
上記のプログラムを実行すると、以下のような図がプロットされます。
上から、インパルス信号、ステップ信号、ランプ信号、指数関数となっています。
まとめ
本記事では、ディジタル信号処理において基本的な信号の生成をPythonを用いて行いました。



コメント