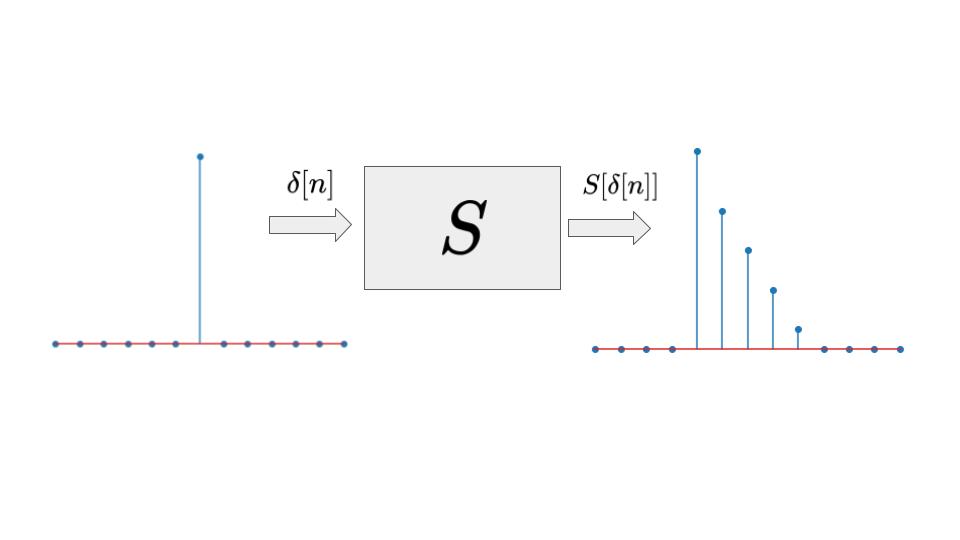
インパルス応答
線形時不変(LTI)システムに単位インパルス信号\(\delta[n]\)を入力したときの出力をインパルス応答といいます。インパルス応答はLTIシステムの振る舞いを知るために重要な要素です。なぜかというと、インパルス応答がわかれば、システムのふるまいを予測することができるからです。
単位インパルス\(\delta[n]\)を用いると任意の信号\(x[n]\)を次式で表現することができます。
$$x[n] = \sum_{k=-\infty}^{\infty} x[k] \delta[n-k]$$
ここで、インパルス信号\(\delta[n]\)に対する、LTIシステム\(S[]\)の応答を\(h[n] = S[\delta[n]\)とすると、時不変より\(\delta[n-k]\)に対する応答は
$$h[n-k] = S[\delta[n-k]]$$
で表されます。これは、インパルス信号を遅らせて入力すると、その応答も遅れて出力されることを意味します。
畳み込み
この式を、任意の入力\(x[n]\)に対する出力\(y[n]\)に対する式に代入すると、
$$y[n] = S[x[n]] = S[\sum_{k=-\infty}^{\infty} x[k] \delta[n-k]]$$
で表されます。
さらに、線形性により、入力を時間について\(k\)だけ移動して、\(x[k]\)倍することを考えると、
$$y[n] = S[x[n]] = \sum_{k=-\infty}^{\infty} x[k] S[\delta[n-k]] = \sum_{k=-\infty}^{\infty} x[k] h[n-k]$$
となる。\(x[k]\)はある時間\(k\)についての入力信号の値なので、定数倍と考えることができます。
この\(x[n]\)と\(h[n]\)に対して、\(y[n]\)を求める上の式の右辺の演算は畳み込み、あるいは畳み込み和と呼ばれます。
畳み込みは次式のように*を用いて表現されることが多いです。
$$y[n] = x[n] * h[n] = \sum_{k=-\infty}^{\infty} x[k] h[n-k]$$
この式から、システムの入出力関係はインパルス応答\(h[n]\)がわかれば、出力\(y[n]\)が完全に予測することができることがわかります。
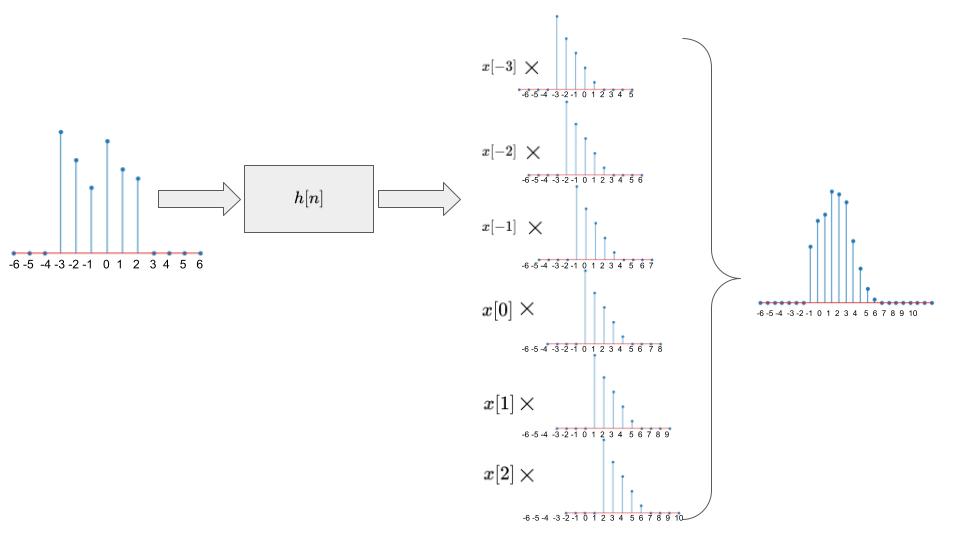
畳み込みの計算イメージ
畳み込み和のイメージ図を下図に示します。上の図のようなインパルス応答を持つシステムに対して、下図のような左にある信号を入力した場合、右側のような出力になります。各時間の入力に対して、それぞれインパルス応答が出力され、それぞれの和が出力されています。
畳み込みの計算例
入力信号\(x[n]\)、インパルス応答\(h[n]\)が下記のような場合を考えます。
$$h[n] = [1, 3, 1]$$
$$x[n] = [2, 1, 5, 3]$$
| \(n\) | 0 | 1 | 2 | 3 | 4 | 5 |
| \(h\times x[0]\) | 1 × 2 | 3 × 2 | 1 × 2 | |||
| \(h\times x[1]\) | 1 × 1 | 3 × 1 | 2 × 1 | |||
| \(h\times x[2]\) | 1 × 5 | 3 × 5 | 1 × 5 | |||
| \(h\times x[3]\) | 1 × 3 | 3 × 3 | 1 × 3 | |||
| \(y\) | 2 | 7 | 10 | 20 | 14 | 3 |
このことからわかるように、畳み込みは出力信号の長さが入力信号より長くなっていることがわかります。出力信号の長さはインパルス応答長を\(N\), 入力信号の長さを\(L\)とすると、
$$L+N-1$$
で出力信号の長さが決定されます。



コメント