ディジタル信号処理　離散時間信号における周期信号

周期信号

まずは、周期信号の定義をしておきます。

ある正の整数\(N\)に対して、

$$x[n]=x[n+N]$$

となるとき、信号\(x[n]\)は周期的という。また、この関係を満たす最小の正の整数\(N_0\)を基本周期、または単に周期と呼びます。

cosとsin

まず、cosとsinの信号の定義を以下に示します。

$$x[n] = A \cos(\omega n + \theta)$$

ここで、\(A\)は振幅、\(\omega\)は角周波数[rad]、\(\theta\)は初期位相[rad]を表します。また、角周波数\(\omega = 2\pi f\)で表され、\(f\)は周波数[rad/s]を表します。

sinは次式で定義されます。

$$x[n] = A \sin(\omega n + \theta)$$

離散信号の周期性

離散信号のsin, cosはある特定の周波数\(\omega\)[rad]をもつときに限って周期的になることを解説していきます。

まず、周期信号の定義よりcosは次式で表されます。cosは\(x[n] = \cos\omega n\)なので、

\begin{eqnarray}
x[n+N] &=& \cos(\omega(n+N)) \\
&=& \cos(\omega n + \omega N)
\end{eqnarray}

となります。

つまり、\(\omega N = 2\pi k \)となるときに限って（\(\frac{2\pi}{\omega} = \frac{N}{k}\)が有理数になるときに限って）、周期的になることがわかります。ここで、kは非ゼロの整数です。ここで、三角関数の性質である、\(\cos(\theta + 2k\pi) = \cos\theta\)を利用しています。

離散信号では、\(n, P\)は整数という制約があるため、\(\omega n, \omega P\)は飛び飛びの離散的な値しか取ることができません。従って、連続信号と異なり、ある特定の\(\omega\)の時のみ周期的という制約が課されます。\(P = \frac{2\pi}{\omega}\)が整数となる必要がありますので、\(\omega N = 2\pi k \)より\(\frac{2\pi}{\omega} = \frac{N}{k}\)が導き出されます。\(P, k\)は整数なので、整数を整数で割ったものは有理数なので、\(\frac{2\pi}{\omega} = \frac{N}{k}\)が有理数になるときに限って周期的になるということです。

この点は、連続時間信号の\(cos(\Omega t), sin(\Omega t)\)が、全ての周波数\(\Omega\)[rad/s]で時刻\(t\)に関して、周期的なことと異なります。

上記のような周期性を考えると、離散時間信号の三角関数はある特定の範囲だけ見れば良さそうだということがわかります。なぜなら、離散時間信号では\(\omega\)を\(2\pi k\)(kは整数)増やす、もしくは減らすと同じ信号になるからです。それは、\(0\leq\omega < 2\pi\)あるいは、\(-\pi\leq \omega< \pi\)の範囲を考えればいいです。この範囲に関しては、対称性を考慮して\(-\pi\leq \omega< \pi\)の範囲が用いられることが多いです。

この点も、連続時間信号が周波数の領域として実数全体であることに対して異なります。

周期性のプロット

import numpy as np
import matplotlib.pyplot as plt
n = np.arange(0, 64)
omega = 2*np.pi / 10

fig, axes = plt.subplots(11, 2, sharex=True)
fig.set_figwidth(10)
fig.set_figheight(10)
k = 0
for i in range(0, 11):
  x = np.cos(n*omega*k)
  axes[i, 0].stem(n, x)
  axes[i, 0].set_title(f"$\omega$ = $2\pi$/10 × {k}")
  k = k + 1
k = 10
for i in range(10, 21, 1):
  x = np.cos(n*omega*k)
  axes[i-10, 1].stem(n, x)
  axes[i-10, 1].set_title(f"$\omega$ = $2\pi$/10 × {k}")
  k = k + 1
plt.tight_layout()

上記のプログラムを実行し以下のような図をプロットしてみると、離散時間信号の周期性を視覚的にみることができます。

上の図をみると、\(2\pi\)増加すると同じ信号になっていることがわかります。角周波数を増やしているはずなのに、実際には周波数は\(2\pi\)増加する前と同じものとなっています。これが連続時間信号と異なる点です。

また、\(0\leq \omega < 2\pi\)においても振動数が単調増加するではないことがわかります。\(0\leq \omega < \pi\)の範囲では振動数が単調増加していますが、一方で\(\pi\leq \omega < 2\pi\)の範囲では振動数が単調減少することがわかります。0, \(2\pi, 4\pi\)は直流成分を表しています。さらに、振動数が一番大きい点は\(\pi\)のときであることがわかります。この値を境に振動数が増えたり減ったりしていることがわかります。先ほどの対称性ということは直流成分を0として考えると、この一番振動数が大きい値を軸の端にして考えることができるので用いられています。

対称性についての補足

import numpy as np
import matplotlib.pyplot as plt
n = np.arange(0, 64)
omega = 2*np.pi / 10 - np.pi

fig, axes = plt.subplots(9, 1, sharex=True)
fig.set_figwidth(10)
fig.set_figheight(10)
k = 1
for i in range(0, 9):
  x = np.cos(n*omega*k)
  axes[i].stem(n, x)
  axes[i].set_title(f"$\omega$ = $2\pi$/10 × {k} - $\pi$")
  k = k + 1
plt.tight_layout()

上記のプログラムを実行すると以下のような図がプロットされます。

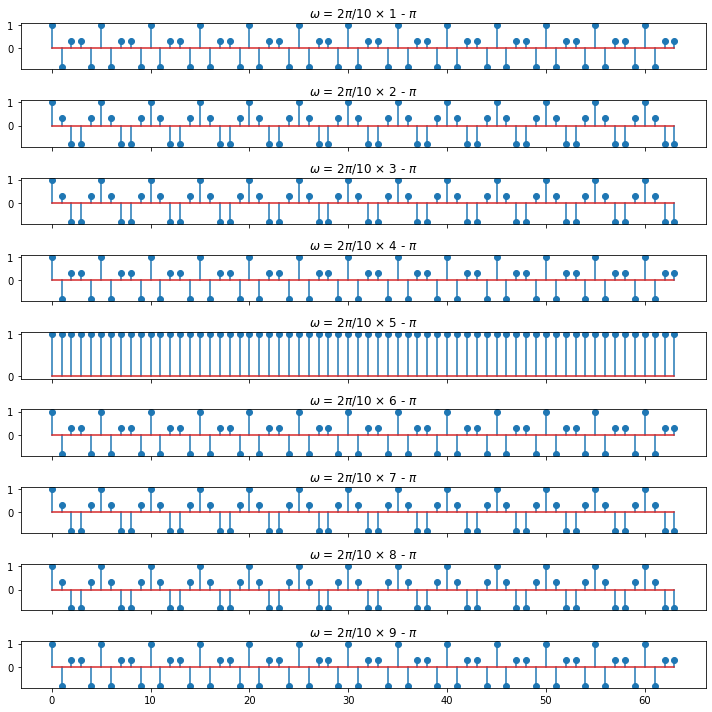
直流成分を境にして、-方向の角周波数では値が小さくなるほど振動数が増えていき、+方向の角周波数では値が大きくなるほど振動数が増えていくことがわかります。このように直流成分を境目にして考えることができるため、一般的に\(-\pi\leq \omega< \pi\)の範囲を考えることが多いです。

まとめ

本記事では、周期信号についての定義し、離散時間信号において三角関数のsin, cosはある特定の周波数を持つときに限って周期的となることを解説しました。