目次
畳み込み積分の性質
畳み込み積分は下記に示す性質を持ちます。
交換則
$$x[n]*h[n] = h[n] * x[n]$$
結合則
$$x[n] * \{h_1[n] * h_2[n]\} = \{x[n] * h_1[n]\} * h_2[n]$$
分配則
$$x[n] * \{h_1[n] + h_2[n]\} = x[n] * h_1[n] + x[n] * h_2[n]$$
フィルタの縦続接続と並列接続
二つのディジタルフィルタ\(S_1, S_2\)のインパルス応答をそれぞれ\(h_1[n], h_2[n]\)とする場合のことを考えます。
縦続接続
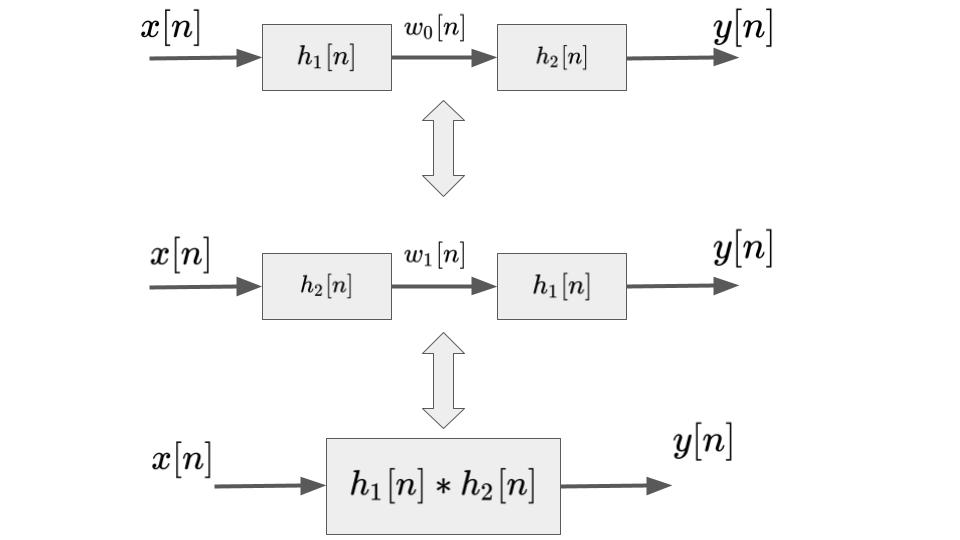
フィルタの縦続接続は下図のような、2つのフィルタを直列に接続するような場合を言います。カスケード接続と呼ばれることもあります。
フィルタの縦続接続は次式のように表されますが、それぞれ同じ意味を持ちます。上記の畳み込み積分の性質からも成り立つことがわかります。
$$y[n] = h_2[n] * w_0[n], w_0[n] = h_1[n] * x[n]$$
$$y[n] = h_1[n] * w_1[n], w_1[n] = h_2[n] * x[n]$$
$$y[n] = \{h_1[n] * h_2[n]\} * x[n]$$
並列接続
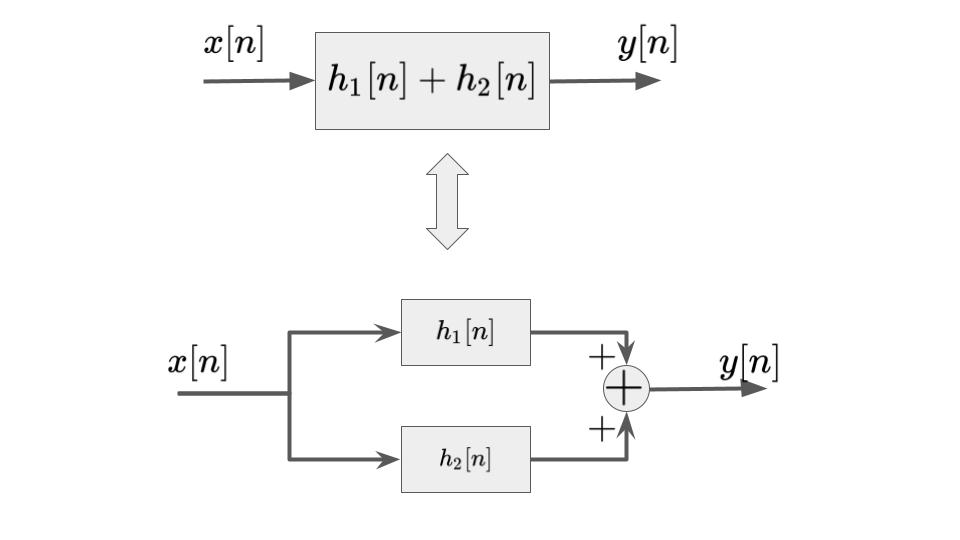
フィルタの並列接続は下図のような、2つのフィルタを並列に接続するような場合を言います。
フィルタの並列接続は次式のように表されますが、それぞれ同じ意味を持ちます。上記の畳み込み積分の性質からも成り立つことがわかります。
$$y[n] = \{h_1[n] + h_2[n]\} * x[n]$$
$$y[n] = h_1[n] * x[n] + h_2[n] * x[n]$$



コメント